Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử mp (a) cắt SA; SB;SC; SD thứ tự tại A'; B'; C'; D'. Tính \(\dfrac{SA}{SA'}+\dfrac{SC}{SC'}-\left(\dfrac{SB}{SB'}+\dfrac{SD}{SD'}\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do AD//BC, M thuộc (SBC) nên giao tuyến của (ADM) với (SBC) là đường thẳng qua M và song song với BC, đường thẳng này cắt SC tại N.
Ta có MN//AD. Vậy thiết diện là hình thang AMND.
Đáp án B

Chọn đáp án A
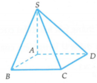
Ta có ABCD là hình bình hành nên CD//AB.
Lại có S A ⊥ A B C D ⇒ S A ⊥ A B
⇒ ∆ S A B vuông tại A.
Suy ra
![]()
Trong tam giác SAB vuông tại A có
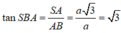
⇒ S B A ⏜ = 60 0

Đáp án D
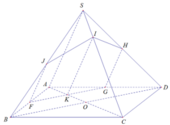
Trong (ABCD), kẻ đường thẳng d đi qua F và song song với BD
d cắt AD tại G
d cắt AC tại K ⇒ F G ∩ A C = K
Trong (SAD), kẻ đường thẳng x đi qua G và song song với SA
x cắt SD tại H
Trong (SAB), kẻ đường thẳng y đi qua F và song song với SA
y cắt SB tại J
Trong (SAC), kẻ đường thẳng z đi qua K và song song với SA
z cắt AC tại I
⇒ FGHIK là thiết diện cần tìm
⇒ thiết diện là ngũ giác

Chọn đáp án A
Áp dụng công thức
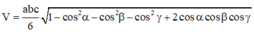
![]()
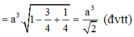
Suy ra V S . A B C D = a 2 2 ( đ v t t )

Đáp án A
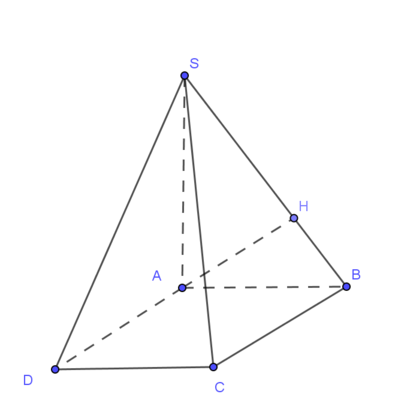
Ta có:
V S . A B C D = 1 3 S A . S A B C D = 1 3 .2 a . a .2 a = 4 3 a 3

Chọn C.
Phương pháp : Dựng thiết diện.
Cách giải : Gọi I, J lần lượt là giao điểm của GF với AB và AD.
Gọi H là giao điểm của IE và SB.
Gọi K là giao điểm của SD và EJ.
Suy ra thiết diện cần tìm là ngũ giác EHFGK.


Trước hết ta chứng minh 1 bổ đề đơn giản về diện tích tam giác như sau (em tự vẽ hình)
Cho tam giác ABC, trên các cạnh AB và AC lần lượt lấy 2 điểm B' và C', khi đó ta có:
\(\dfrac{S_{AB'C'}}{S_{ABC}}=\dfrac{AB'.AC'}{AB.AC}\)
Chứng mình: từ C và C' lần lượt hạ CH và C'H' vuông góc AB, khi đó CH song song C'H' nên theo Talet:
\(\dfrac{C'H'}{CH}=\dfrac{AC'}{AC}\)
\(\Rightarrow\dfrac{S_{AB'C'}}{S_{ABC}}=\dfrac{\dfrac{1}{2}C'H'.AB'}{\dfrac{1}{2}CH.AB}=\dfrac{AC'.AB'}{AC.AB}\)
Quay lại bài, gọi O là tâm đáy
Trong mp (SAC), tại O' là giao điểm của SO và A'C'
Ba mặt phẳng (SAC), (SBD), \(\left(\alpha\right)\) cắt nhau theo 3 giao tuyến phân biệt là SO, A'C', B'D' nên 3 giao tuyến này song song hoặc đồng quy.
Mà SO và A'C' cắt nhau tại O' nên 3 đường thẳng nói trên đồng quy tại O'
Ta có:
\(S_{SA'C'}=S_{SA'O'}+S_{SC'O'}\Rightarrow\dfrac{S_{SA'C'}}{S_{SAC}}=\dfrac{S_{SA'O'}}{S_{SAC}}+\dfrac{S_{SC'O'}}{S_{SAC}}\)
\(\Rightarrow\dfrac{S_{SA'C'}}{S_{SAC}}=\dfrac{S_{SA'O'}}{2S_{SAO}}+\dfrac{S_{SC'O'}}{S_{SCO}}\Rightarrow\dfrac{SA'.SC'}{SA.SC}=\dfrac{SA'.SO'}{2SA.SO}+\dfrac{SC'.SO'}{2SC.SO}\)
\(\Leftrightarrow\dfrac{SA'.SC'}{SA.SC}=\dfrac{SO'}{2SO}\left(\dfrac{SA'}{SA}+\dfrac{SC'}{SC}\right)\)
\(\Leftrightarrow SA'.SC'=\dfrac{SO'}{2SO}\left(SC.SA'+SA.SC'\right)\)
\(\Leftrightarrow1=\dfrac{SO'}{2SO}\left(\dfrac{SC}{SC'}+\dfrac{SA}{SA'}\right)\)
\(\Leftrightarrow\dfrac{SA}{SA'}+\dfrac{SC}{SC'}=\dfrac{2SO}{SO'}\)
Hoàn toàn tương tự, ta cũng có \(\dfrac{SB}{SB'}+\dfrac{SD}{SD'}=\dfrac{2SO}{SO'}\)
\(\Rightarrow\dfrac{SA}{SA'}+\dfrac{SC}{SC'}-\left(\dfrac{SB}{SB'}+\dfrac{SD}{SD'}\right)=0\)