Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta thấy 3x3+4x4=5x5 nên nó là tam giác vuông
diện tích là S=1/2x3x4=6(cm2)
chúc bạn học tốt
HYC-23/1/2022

Xét
DE^2 + DF^2 = 3^2 + 4^2 = 9 + 16 = 25
EF^2 = 5^2 = 5
=> DE^2 + DF^2 = EF^2
=> DEF là tam giác vuông

\(\widehat{D}=180^0-\widehat{E}-\widehat{F}=50^0=\widehat{A}\\ \left\{{}\begin{matrix}AB=DE\\\widehat{A}=\widehat{D}\\AC=DE\end{matrix}\right.\Rightarrow\Delta ABC=\Delta DEF\left(c.g.c\right)\)

xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)
xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông
và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)

\(\Delta DEF\) cho ta \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\)
\(\Rightarrow\widehat{D}=180^0-\left(\widehat{E}+\widehat{F}\right)\)
\(\Rightarrow\widehat{D}=180^0-\left(70^0+60^0\right)=180^0-130^0=50^0\)
\(Xét\) \(\Delta ABCvà\Delta DEFcó\)
\(\widehat{A}=\widehat{D}\left(=50^0\right)\)
AB=DE
AC=DF
\(\Rightarrow\Delta ABC=\Delta DEF\left(c-g-c\right)\)
Vậy \(\Delta ABC=\Delta DEF\)

xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông
và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)
Cho tam giác ABC và tam giác DEF có: AB=DE,BC=EF,AC=DF.
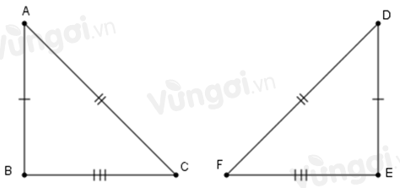
Xét ΔABC và ΔDEF có:
AB=DE(gt)
BC=EF(gt)
AC=DF(gt)
⇒ΔABC=ΔDEF (c.c.c).
Học tốt nhé!

Để hai tam giác trên bằng nhau theo trường hợp c.c.c thì các cặp cạnh tương ứng phải bằng nhau. Vì đã có hai cặp cạnh tương ứng là MN và DE, PM và DF nên cần thêm điều kiện NP = EF để hai tam giác trên bằng nhau theo trường hợp c.c.c
Giải: (hình bn vẽ nha)
a,
- Xét △DEI và △DMI, có:
DE = DM (theo giả thiết)
EI = MI (theo giả thiết)
DI_cạnh chung
=> △DEI = △DMI (c.c.c)
b,
- Có △DEI = △DMI (chứng minh trên)
=> ∠DIE = ∠DIM (2 cạnh tương ứng)
mà 2 góc này kề bù
=> ∠DIE = ∠DIM = \(\dfrac{180^o}{2}\) = \(90^o\)
<=> DI ⊥ EM tại I
c,
- Có \(\left\{{}\begin{matrix}DN=EM\\DI=IH\\DI\text{⊥EM}\end{matrix}\right.\)(theo giả thiết/ chứng minh trên)
=> △DNI = △EIH
Do đó, ta có 3 điểm N, E, H thẳng hàng.