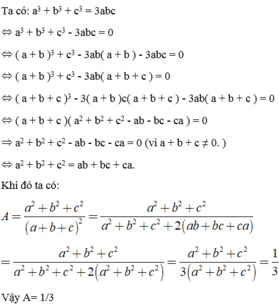Tính giá trị biểu thức Q=a3+b3+c3/abc với a,b,c thoả mãn:(3a-2b)+|4b-3c| ≤ 0.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a+b+c=1\)
\(\Leftrightarrow\left(a+b+c\right)^3=1\)
\(\Leftrightarrow a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(c+a\right)=1\)
\(\Leftrightarrow1+3\left(a+b\right)\left(b+c\right)\left(c+a\right)=1\)'
\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=0\\b+c=0\\c+a=0\end{matrix}\right.\)
Không mất tính tổng quát, giả sử \(a+b=0\), các trường hợp còn lại làm tương tự.
Khi đó từ \(a+b+c=1\) suy ra \(c=1\) (thỏa mãn). Thế thì \(T=0^{2023}+0^{2023}+1^{2023}=1\).
Như vậy \(T=1\)

Do \(0\le a,b,c\le1\)
nên\(\left\{{}\begin{matrix}\left(a^2-1\right)\left(b-1\right)\ge0\\\left(b^2-1\right)\left(c-1\right)\ge0\\\left(c^2-1\right)\left(a-1\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2b-b-a^2+1\ge0\\b^2c-c-b^2+1\ge0\\c^2a-a-c^2+1\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2b\ge a^2+b-1\\b^2c\ge b^2+c-1\\c^2a\ge c^2+a-1\end{matrix}\right.\)
Ta cũng có:
\(2\left(a^3+b^3+c^3\right)\le a^2+b+b^2+c+c^2+a\)
Do đó \(T=2\left(a^3+b^3+c^3\right)-\left(a^2b+b^2c+c^2a\right)\)
\(\le a^2+b+b^2+c+c^2+a\)\(-\left(a^2+b-1+b^2+c-1+c^2+a-1\right)\)
\(=3\)
Vậy GTLN của T=3, đạt được chẳng hạn khi \(a=1;b=0;c=1\)

Ta có
( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 = a 3 + b 3 + 3 a b ( a + b ) = > a 3 + b 3 = ( a + b ) 3 – 3 a b ( a + b )
Từ đó
B = a 3 + b 3 + c 3 – 3 a b c = ( a + b ) 3 – 3 a b ( a + b ) + c 3 – 3 a b c = [ ( a + b ) 3 + c 3 ] – 3 a b ( a + b + c ) = ( a + b + c ) [ ( a + b ) 2 – ( a + b ) c + c 2 ] – 3 a b ( a + b + c )
Mà a + b + c = 0 nên
B = 0 . [ ( a + b ) 2 – ( a + b ) c + c 2 ] – 3 a b . 0 = 0
Vậy B = 0
Đáp án cần chọn là: A