cho tam giác vuông abc vuông tại a đường cao ah đường trung tuyến ao trên tia đối của tiaha lấy điểm d sao co ha=hd, docawts ac tại m chứng minh 4 điểm bằng nhau a b c d
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Đặt AB/3=AC/4=k
=>AB=3k; AC=4k
Xét ΔBAC vuông tại A có \(AB^2+AC^2=BC^2\)
\(\Leftrightarrow25k^2=100\)
=>k=2
=>AB=6cm; AC=8cm
b: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đo: ΔCAD cân tại C
hay CA=CD
Xét ΔBAD có
BH là đườg cao
BH là đường trung tuyến
Do đo:ΔBAD cân tại B
Xét ΔCAB và ΔCDB có
CA=CD
AB=DB
CB chung
Do đó: ΔCAB=ΔCDB
Suy ra: \(\widehat{CAB}=\widehat{CDB}=90^0\)
hay ΔBDC vuông tại D
c: Xét ΔDAE có
C là trung điểm của DE
H là trung điểm của DA
DO đó:CH là đường trung bình
=>CH//AE
hay AE//BC

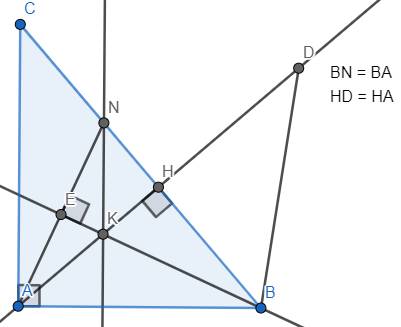
a) Xét ΔABE vuông tại E & ΔNBE vuông tại E có:
- BE là cạnh chung, BN = BA (giả thuyết)
Suy ra ΔABE = ΔNBE (cạnh huyền - cạnh góc vuông)
b) Theo đề ta có BH vuông góc với AD và HA = HD
Suy ra BH là đường trung trực của AD
Suy ra BA = BD (vì B nằm trên đường trung trực của AD)
c) Trong ΔNAB có AH và BE là đường cao, đồng quy tại điểm K
Suy ra NK là đường cao của ΔNAB, hay NK vuông góc với AB
Mà AC cũng vuông góc với AB, suy ra NK // CA
a. - Vì BE vuông góc với AN (gt)
=> tam giác ABE vuông tại E (tc)
tam giác NBE vuông tại E (tc)
- Xét tam giác vuông ABE và tam giác vuông NBE, có:
+ Chung BE
+ BA = BN (gt)
=> tam giác vuông ABE = tam giác vuông NBE (Cạnh huyền - cạnh góc vuông)
b. - Vì AH là đường cao của tam giác ABC (gt)
=> tam giác ABH vuông tại H
tam giác DBH vuông tại H
- Xét tam giác vuông ABH và tam giác vuông DBH, có:
+ Chung BH
+ HA = HD (gt)
=> tam giác vuông ABH = tam giác vuông DBH (2 cạnh góc vuông)
=> BA = BD (2 cạnh tương ứng)

a)
Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(hai cạnh tương ứng)
Xét ΔABH vuông tại H và ΔDCH vuông tại D có
AH=DH(gt)
BH=CH(cmt)
Do đó: ΔABH=ΔDCH(hai cạnh góc vuông)
Suy ra: AB=DC(Hai cạnh tương ứng)
mà AB=AC(ΔABC cân tại A)
nên AC=DC(đpcm)
b) Xét ΔAHE vuông tại H và ΔDHE vuông tại H có
EH chung
AH=DH(gt)
Do đó: ΔAHE=ΔDHE(hai cạnh góc vuông)
Suy ra: AE=DE(Hai cạnh tương ứng)
Xét ΔACE và ΔDCE có
CA=CD(cmt)
CE chung
AE=DE(cmt)
Do đó: ΔACE=ΔDCE(c-c-c)

a: Xét ΔBEA vuông tại E và ΔBEN vuông tại Ecó
BE chung
BA=BN
=>ΔBEA=ΔBEN
b: Xet ΔBAD co
BH vừa là đường cao, vừa là trung tuyến
=>ΔBAD cân tại B
=>BA=BD
c: Xet ΔNAB có
AH,BE là đường cao
AH cắt BE tại K
=>K là trực tâm
=>NK vuông góc AB
=>NK//AC

a: Xét ΔBEA vuông tại E và ΔBEN vuông tại E co
BA=BN
BE chung
=>ΔBEA=ΔBEN
b: Xét ΔBAD có
BH vừa là đường cao, vừa là đường trung tuyến
=>ΔBAD cân tại B
c: Xét ΔNAB có
AH,BE là đường cao
AH cắt BE tại K
=>K là trực tâm
=>NK vuông góc AB
=>NK//AC

1) Xét ΔCDE vuông tại D và ΔAHB vuông tại H có
\(\widehat{DCE}=\widehat{HAB}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔCDE\(\sim\)ΔAHB(g-g)
Đề sai rồi em!