Để đo chiều rộng AB của 1 khúc sông mà ko phải băng qua nó, người ta xác định điểm C sao cho AC= 60m. Từ C nhìn thấy B một góc ACB theo phương bằng 50 độ. Tính chiều rộng khúc sông ( Kết quả làm tròn đến chữ số thập phân thứ 2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
tan C = AB/AC
AB = AC.tan C
= 60.tan 50⁰
≈ 71,51 (m)
Vậy chiều rộng khúc sông là 71,51 m

Ta có:
tan ACB = AB/AC
⇒ AB = AC.tan ACB
= 60.tan 50⁰
≈ 71,51 (m)
Vậy chiều rộng của khúc sông là 71,51 m

+ Mô tả cách làm:
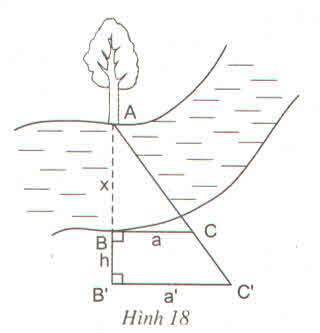
- Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và AB chính là khoảng cách cần đo.
- Trên hai đường thẳng vuông góc với AB' tại B và B' lấy C và C' thằng hàng với A.
- Đo độ dài các đoạn BB' = h, BC = a, B'C' = a' ta sẽ tính được đoạn AB.
+ Cách tính AB.
Ta có: BC ⊥ AB’ và B’C’ ⊥ AB’ ⇒ BC // B’C’
ΔAB’C’ có BC // B’C’ (B ∈ AB’, C ∈ AC’)
⇒ 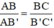 (hệ quả định lý Talet)
(hệ quả định lý Talet)
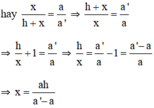

Ta có hình như sau :
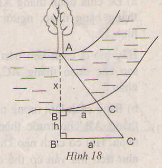
giải :
Ta có:
=
mà AB' = x + h nên
=
<=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=
Vậy khoảng cách AB bằng
Ta có hình như sau :

Giải
Ta có:
=
mà AB' = x + h nên
=
<=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=
Vậy khoảng cách AB bằng

Gọi AB là đoạn đường mà con thuyền đi được trong 6p, BH là chiều rộng của khúc sông
=>ΔBHA vuông tại H
AB=20*1/10=2(km)=2000(m)
Xét ΔBHA vuông tại H có BH=BA*sinA
=>\(BH=2000\cdot sin40\simeq1285,58\left(m\right)\)

Ta có:
= mà AB' = x + h nên
= <=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=
Vậy khoảng cách AB bằng
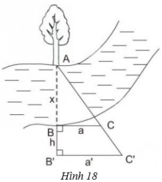
Ta có:
tan C = AB/AC
AB = AC.tan C
= 60.tan 50⁰
≈ 71,51 (m)
Vậy chiều rộng khúc sông là 71,51 m