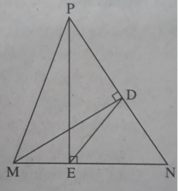
Cho tam giác MNP nhọn(ME<MP).Vẽ MD là phân giác của góc NMP D thuộc NP.Trên cạnh MP lấy điểm E sao cho ME=MN.
a,CM:Hình tam giác MND=hình tam giác MED
b,CM:Tam giác NDE cân tại D.
c,Tam giác MEN là tam giác gì?Khi góc MEN=60 độ
d,CM:MD là đường trung trực của đoạn thẳng NE.


⇒ ∠NMD = ∠PMD
⇒ ∠NMD = ∠EMD
Xét ∆MND và ∆MED có:
MN = ME (gt)
∠NMD = ∠EMD (cmt)
MD là cạnh chung
⇒ ∆MND = ∆MED (c-g-c)
b) Do ∆MND = ∆MED (cmt)
ND = ED (hai cạnh tương ứng)
⇒ ∆NDE cân tại D
c) Do MN = ME (gt)
⇒ ∆MNE cân tại M
Mà ∠MEN = 60⁰ (gt)
⇒ ∆MEN là tam giác đều
d) Gọi A là giao điểm của NE và MD
Do ∠NMD = ∠EMD (cmt)
⇒ ∠NMA = ∠EMA
Xét ∆MNA và ∆MEA có:
MA là cạnh chung
∠NMA = ∠EMA (cmt)
MN = ME (gt)
⇒ ∆MNA = ∆MEA (c-g-c)
⇒ ∠MAN = ∠MAE (hai góc tương ứng)
Mà ∠MAN + ∠MAE = 180⁰ (kề bù)
⇒ ∠MAN = ∠MAE = 180⁰ : 2 = 90⁰
⇒ MA ⊥ NE (1)
Do ∆MNA = ∆MEA (cmt)
⇒ NA = EA (hai cạnh tương ứng)
⇒ A là trung điểm của NE (2)
Từ (1) và (2) ⇒ MA là đường trung trực của NE
Hay MD là đường trung trực của NE
a: Sửa đề: MN<MP
Xét ΔMND và ΔMED có
MN=ME
\(\widehat{NMD}=\widehat{EMD}\)
MD chung
Do đó: ΔMND=ΔMED
b: Ta có: ΔMND=ΔMED
=>DN=DE
=>ΔDNE cân tại D
c: Xét ΔMNE có MN=ME
nên ΔMNE cân tại M
Xét ΔMNE cân tại M có \(\widehat{NME}=60^0\)
nên ΔMNE đều
d: Ta có: MN=ME
=>M nằm trên đường trung trực của NE(1)
Ta có: DN=DE
=>D nằm trên đường trung trực của NE(2)
Từ (1) và (2) suy ra MD là đường trung trực của NE