trình bày ra giúp e 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

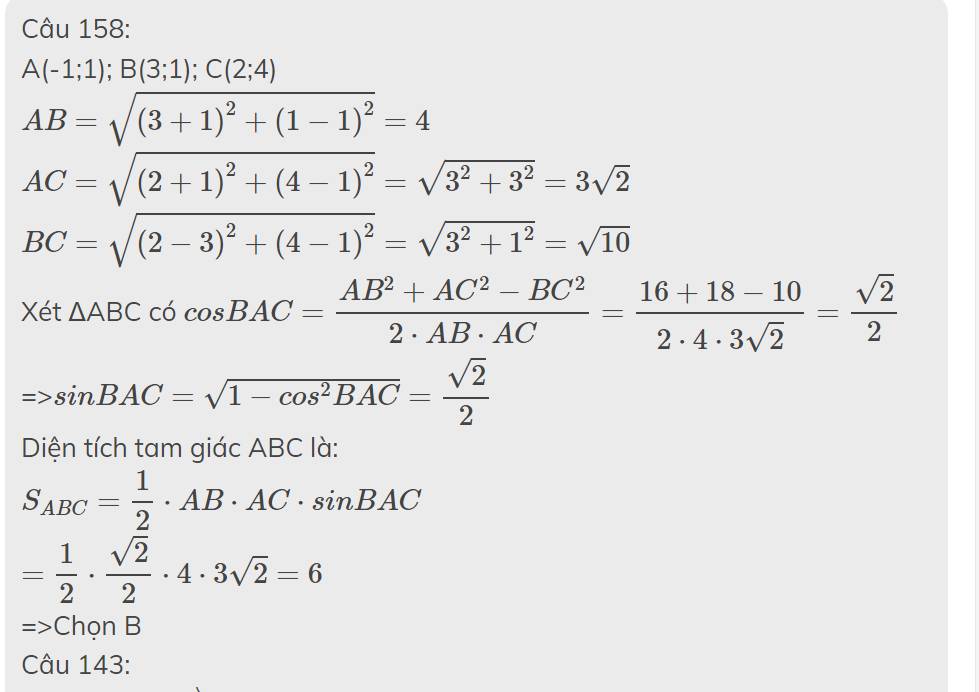
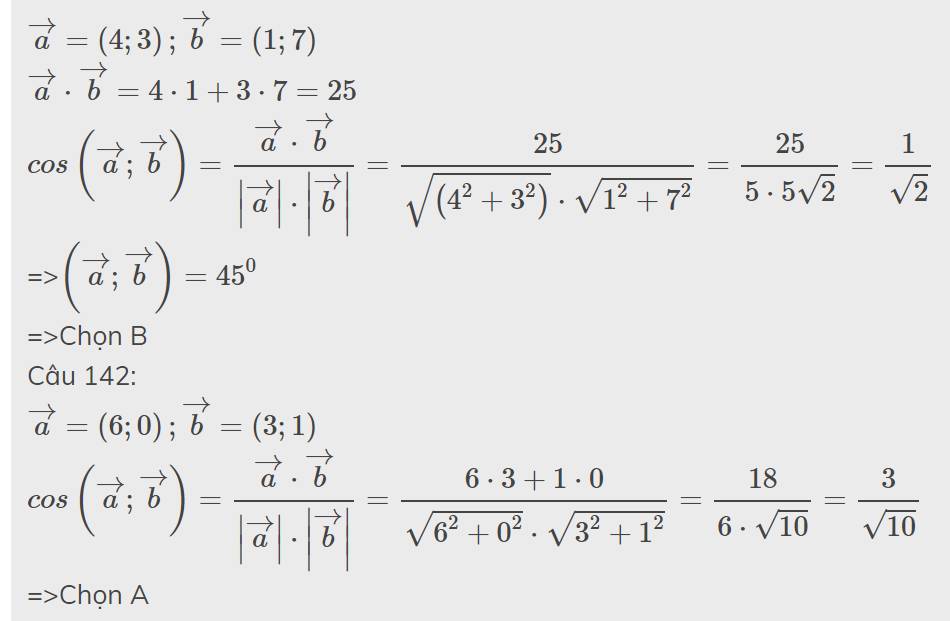
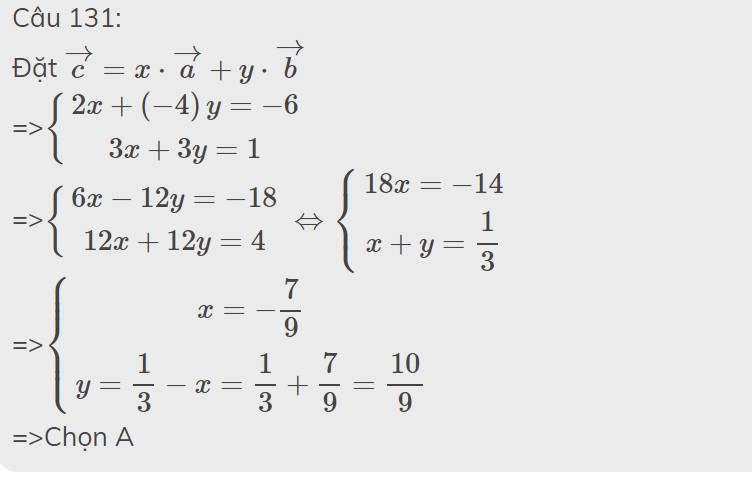

Câu 393:
Ta có: \(n_{Mg}=\dfrac{5,76}{24}=0,24\left(mol\right)\)
\(n_{Zn}=\dfrac{17,55}{65}=0,27\left(mol\right)\)
BTNT Mg: nMg(NO3)2 = nMg = 0,24 (mol)
BTNT Zn: nZn(NO3)2 = nZn = 0,27 (mol)
Có: mMg(NO3)2 + mZn(NO3)2 + mNH4NO3 = 89,75
⇒ mNH4NO3 = 3,2 (g)
\(\Rightarrow n_{NH_4NO_3}=\dfrac{3,2}{80}=0,04\left(mol\right)\)
1. BT e, có: 2nMg + 2nZn + 10nN2 + 8nNH4NO3
⇒ nN2 = 0,07 (mol)
⇒ VN2 = 0,07.22,4 = 1,568 (l)
→ Đáp án: B
2. nHNO3 = 12nN2 + 10nNH4NO3 = 1,24 (mol)
\(\Rightarrow m_{ddHNO_3}=\dfrac{1,24.63}{31,5\%}=248\left(g\right)\)
→ Đáp án: B
Câu 394:
Ta có: \(n_{Mg}=\dfrac{6,48}{24}=0,27\left(mol\right)\)
\(n_{Zn}=\dfrac{16,25}{65}=0,25\left(mol\right)\)
BTNT Mg: nMg(NO3)2 = nMg = 0,27 (mol)
BTNT Zn: nZn(NO3)2 = nZn = 0,25 (mol)
⇒ mMg(NO3)2 + nZn(NO3)2 + mNH4NO3 = 91,21
⇒ nNH4NO3 = 0,05 (mol)
1. BT e, có: 2nMg + 2nZn = 8nN2O + 8nNH4NO3
⇒ nN2O = 0,08 (mol)
⇒ VN2O = 0,08.22,4 = 1,792 (l)
→ Đáp án: A
2. nHNO3 = 10nN2O + 10nNH4NO3 = 1,3 (mol)
\(\Rightarrow m_{ddHNO_3}=\dfrac{1,3.63}{25,2\%}=325\left(g\right)\)
→ Đáp án: B

Câu 347:
Coi A gồm: Cu, Fe và O.
Ta có: \(n_{HNO_3}=1,1.2=2,2\left(mol\right)\)
\(n_{NO_2}=\dfrac{8,96}{22,4}=0,4\left(mol\right)\)
BT e, có: 2nCu + 3nFe - 2nO = nNO2 = 0,4 (1)
BTNT Cu: nCu(NO3)2 = nCu
BTNT Fe: nFe(NO3)3 = nFe
⇒ 188nCu + 242nFe = 153,2 (2)
BTNT N, có: nHNO3 = 2nCu(NO3)2 + 3nFe(NO3)2 + nNO2
⇒ 2nCu + 3nFe = 2,2 - 0,4 (3)
Từ (1), (2) và (3) \(\Rightarrow\left\{{}\begin{matrix}n_{Cu}=0,3\left(mol\right)\\n_{Fe}=0,4\left(mol\right)\\n_O=0,7\left(mol\right)\end{matrix}\right.\)
1. m = mCu + mFe + mO = 52,8 (g)
→ Đáp án: C
2. mCu(NO3)2 = 0,4.188 = 75,2 (g)
→ Đáp án: B
Câu 346 mình đã làm ở trên rồi nhé.

Câu 348:
Coi A gồm: Cu, Fe và O.
Ta có: nH2SO4 = 0,5.4 = 2 (mol)
\(n_{SO_2}=\dfrac{8,96}{22,4}=0,4\left(mol\right)\)
BT e, có: 2nCu + 3nFe - 2nO = 2nSO2 = 0,8 (1)
BTNT Cu: nCuSO4 = nCu
BTNT Fe: nFe2(SO4)3 = 1/2nFe
⇒ 160nCu + 200nFe = 224 (2)
BTNT S, có: nH2SO4 = nCuSO4 + 3nFe2(SO4)3 + nSO2
⇒ nCu + 3/2nFe + 0,4 = 2 (3)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{Cu}=0,4\left(mol\right)\\n_{Fe}=0,8\left(mol\right)\\n_O=1,2\left(mol\right)\end{matrix}\right.\)
1. m = mCu + mFe + mO = 89,6 (g)
→ Đáp án: D
2. mCuSO4 = 0,4.160 = 64 (g)
→ Đáp án: A

Câu 388 mình đã làm ở trên rồi nhé.
Câu 387:
Ta có: \(n_{Mg}=\dfrac{3,6}{24}=0,15\left(mol\right)\)
\(n_{Al}=\dfrac{8,1}{27}=0,3\left(mol\right)\)
Có: \(\left\{{}\begin{matrix}n_{N_2}+n_{N_2O}=\dfrac{1,792}{22,4}=0,08\\28n_{N_2}+44n_{N_2O}=0,08.18.2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}n_{N_2}=0,04\left(mol\right)\\n_{N_2O}=0,04\left(mol\right)\end{matrix}\right.\)
BT e, có: 2nMg + 3nAl = 10nN2 + 8nN2O + 8nNH4NO3
⇒ nNH4NO3 = 0,06 (mol)
1. BTNT Mg: nMg(NO3)2 = nMg = 0,15 (mol)
BTNT Al: nAl(NO3)3 = nAl = 0,3 (mol)
⇒ m = mMg(NO3)2 + mAl(NO3)3 + mNH4NO3 = 90,9 (g)
→ Đáp án: D
2. nHNO3 = 12nN2 + 10nN2O + 10nNH4NO3 = 1,48 (mol)
\(\Rightarrow m_{ddHNO_3}=\dfrac{1,48.63}{15,75\%}=592\left(g\right)\)
→ Đáp án: D

Câu 388:
mFe (dư) = 2,8 (g) \(\Rightarrow n_{Fe\left(dư\right)}=\dfrac{2,8}{56}=0,05\left(mol\right)\)
⇒ nFe (pư) = 0,35 - 0,05 = 0,3 (mol)
BT e, có: 2nMg + 2nFe = 8nN2O + 3nNO + 8nNH4NO3
⇒ nNH4NO3 = 0,025 (mol)
1. Ta có: nHNO3 = 10nN2O + 4nNO + 10nNH4NO3 = 1,15 (mol)
\(\Rightarrow m_{ddHNO_3}=\dfrac{1,15.63}{21\%}=345\left(g\right)\)
→ Đáp án: C
2. BTNT Mg: nMg(NO3)2 = nMg = 0,15 (mol)
BTNT Fe: nFe(NO3)2 = nFe = 0,3 (mol)
m muối = mMg(NO3)2 + mFe(NO3)2 + mNH4NO3 = 78,2 (g) = a
→ Đáp án: B
Câu 383:
Ta có: \(n_{Al}=\dfrac{5,4}{27}=0,2\left(mol\right)\)
\(n_{Zn}=\dfrac{19,5}{65}=0,3\left(mol\right)\)
\(n_{N_2O}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
BT e, có: \(3n_{Al}+2n_{Zn}=8n_{N_2O}+8n_{NH_4NO_3}\)
\(\Rightarrow n_{NH_4NO_3}=0,05\left(mol\right)\)
1. BTNT Al: nAl(NO3)3 = nAl = 0,2 (mol)
BTNT Zn: nZn(NO3)2 = nZn = 0,3 (mol)
⇒ m = mAl(NO3)3 + mZn(NO3)2 + mNH4NO3 = 103,3 (g)
→ Đáp án: C
2. Ta có: nHNO3 = 10nN2O + 10nNH4NO3 = 1,5 (mol)
\(\Rightarrow m_{ddHNO_3}=\dfrac{1,5.63}{12,6\%}=750\left(g\right)\)
→ Đáp án: A

Câu 170:
Gọi $H(a,b)$ là tọa độ trực tâm của tam giác $ABC$
Có:
$AH\perp BC$
$\Leftrightarrow \overrightarrow{AH}.\overrightarrow{BC}=0$
$\Leftrightarrow (a+3, b-6).(-14,14)=0$
$\Leftrightarrow -14(a+3)+14(b-6)=0$
$\Leftrightarrow -a-3+b-6=0$
$\Leftrightarrow -a+b=9(1)$
$BH\perp AC$
$\Leftrightarrow \overrightarrow{BH}.\overrightarrow{AC}=0$
$\Leftrightarrow (a-9, b+10).(-2, -2)=0$
$\Leftrightarrow -2(a-9)-2(b+10)=0$
$\Leftrightarrow a-9+b+10=0$
$\Leftrightarrow a+b=-1(2)$
Từ $(1); (2)\Rightarrow a=-5; b=4$
Đáp án C.
Câu 189:
Gọi $I(a,b)$ là tâm đường tròn ngoại tiếp tam giác $ABC$.
$M(\frac{3}{2}, \frac{-1}{2}), N(\frac{5}{2}, \frac{1}{2})$ lần lượt là trung điểm của $AB, BC$
Có:
$IM\perp AB$
$\Leftrightarrow \overrightarrow{MI}.\overrightarrow{AB}=0$
$\Leftrightarrow (a-\frac{3}{2}, b+\frac{1}{2}).(-1, -3)=0$
$\Leftrightarrow -(a-\frac{3}{2})-3(b+\frac{1}{2})=0$
$\Leftrightarrow a-\frac{3}{2}+3b+\frac{3}{2}=0$
$\Leftrightarrow a+3b=0(1)$
Lại có:
$IN\perp BC$
$\Leftrightarrow \overrightarrow{NI}.\overrightarrow{BC}=0$
$\Leftrightarrow (a-\frac{5}{2}, b-\frac{1}{2})(3,5)=0$
$\Leftrightarrow 3(a-\frac{5}{2})+5(b-\frac{1}{2})=0$
$\Leftrightarrow 3a+5b=10(2)$
Từ $(1); (2)\Rightarrow a=\frac{15}{2}; b=\frac{-5}{2}$
Đáp án A.

Câu 158:
A(-1;1); B(3;1); C(2;4)
\(AB=\sqrt{\left(3+1\right)^2+\left(1-1\right)^2}=4\)
\(AC=\sqrt{\left(2+1\right)^2+\left(4-1\right)^2}=\sqrt{3^2+3^2}=3\sqrt{2}\)
\(BC=\sqrt{\left(2-3\right)^2+\left(4-1\right)^2}=\sqrt{3^2+1^2}=\sqrt{10}\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{16+18-10}{2\cdot4\cdot3\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
=>\(sinBAC=\sqrt{1-cos^2BAC}=\dfrac{\sqrt{2}}{2}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\cdot4\cdot3\sqrt{2}=6\)
=>Chọn B
Câu 143:
\(\overrightarrow{a}=\left(4;3\right);\overrightarrow{b}=\left(1;7\right)\)
\(\overrightarrow{a}\cdot\overrightarrow{b}=4\cdot1+3\cdot7=25\)
\(cos\left(\overrightarrow{a};\overrightarrow{b}\right)=\dfrac{\overrightarrow{a}\cdot\overrightarrow{b}}{\left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|}=\dfrac{25}{\sqrt{\left(4^2+3^2\right)}\cdot\sqrt{1^2+7^2}}=\dfrac{25}{5\cdot5\sqrt{2}}=\dfrac{1}{\sqrt{2}}\)=>\(\left(\overrightarrow{a};\overrightarrow{b}\right)=45^0\)
=>Chọn B
Câu 142:
\(\overrightarrow{a}=\left(6;0\right);\overrightarrow{b}=\left(3;1\right)\)
\(cos\left(\overrightarrow{a};\overrightarrow{b}\right)=\dfrac{\overrightarrow{a}\cdot\overrightarrow{b}}{\left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|}=\dfrac{6\cdot3+1\cdot0}{\sqrt{6^2+0^2}\cdot\sqrt{3^2+1^2}}=\dfrac{18}{6\cdot\sqrt{10}}=\dfrac{3}{\sqrt{10}}\)
=>Chọn A
Câu 131:
Đặt \(\overrightarrow{c}=x\cdot\overrightarrow{a}+y\cdot\overrightarrow{b}\)
=>\(\left\{{}\begin{matrix}2x+\left(-4\right)y=-6\\3x+3y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6x-12y=-18\\12x+12y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}18x=-14\\x+y=\dfrac{1}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{7}{9}\\y=\dfrac{1}{3}-x=\dfrac{1}{3}+\dfrac{7}{9}=\dfrac{10}{9}\end{matrix}\right.\)
=>Chọn A









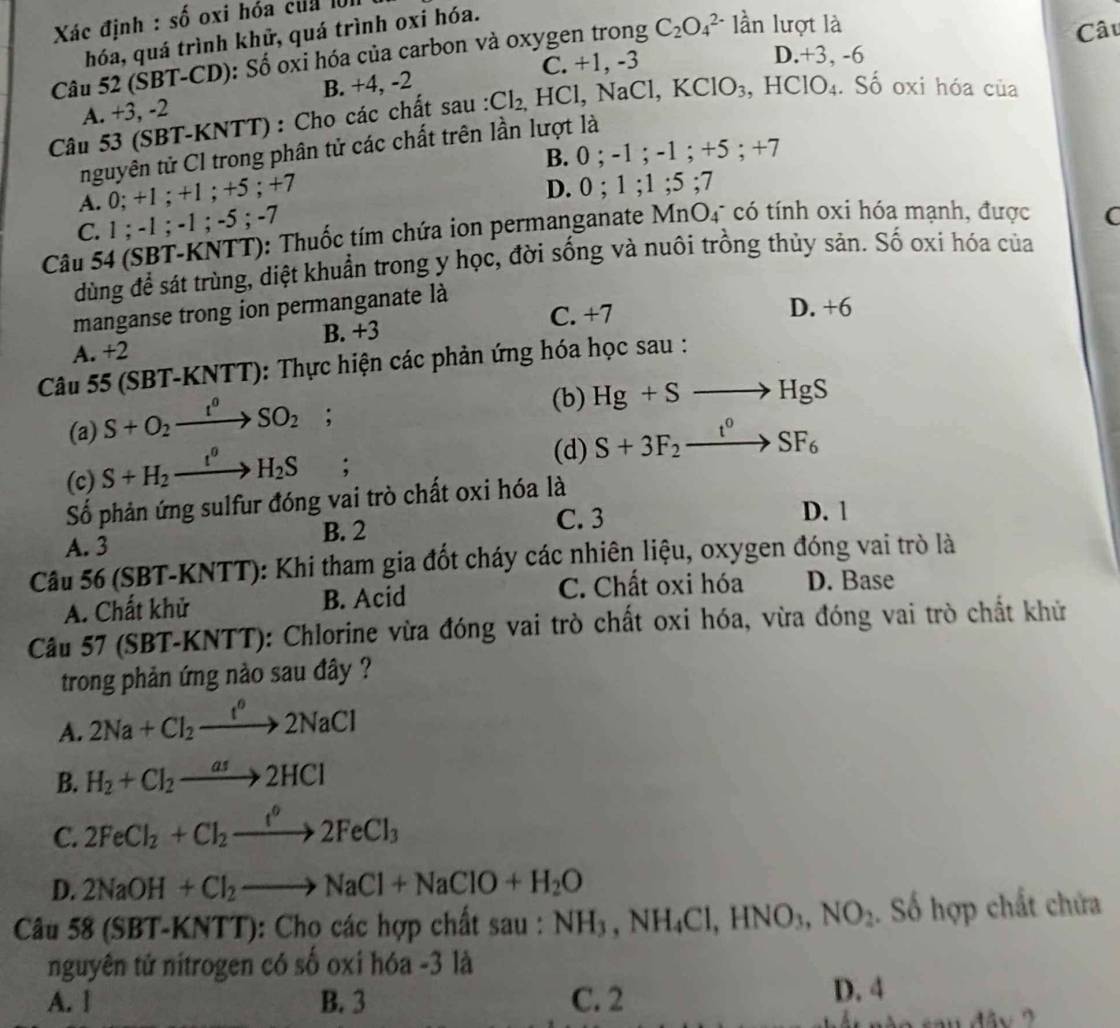

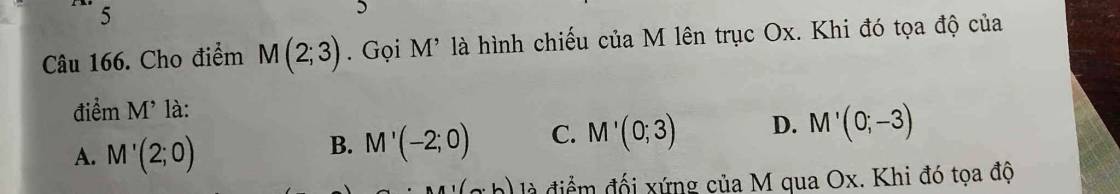
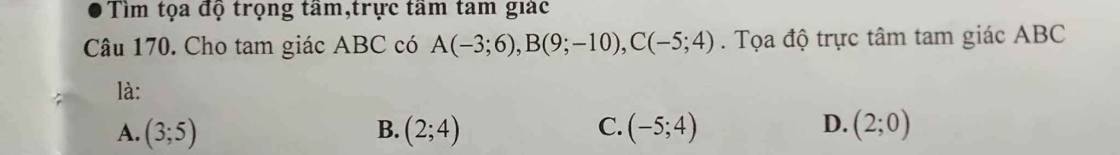
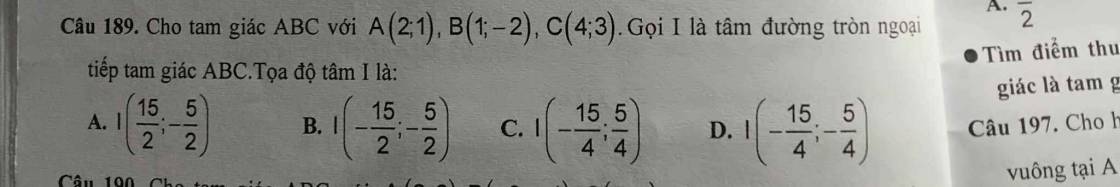
 mn trình bày rõ ra giúp e vs e cảm ơn
mn trình bày rõ ra giúp e vs e cảm ơn