 giúp em với ạ, mai em thi rồi
giúp em với ạ, mai em thi rồi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Công thức tính lực đẩy Achimedes:
FA = d . V
Trong đó:
FA là Lực đẩy Achimedes (đơn vị N)
d là khối lượng riêng của chất lỏng (đơn vị N/m3)
V là thể tích phần chất lỏng bị chiếm chỗ (đơn vị m3)



1 The distance from my home to school is about 3 km
2 My mum used to live in a small village when she was small
3 Despite being a millionaire , he lives in a small flat
4 when does the festive take place ?
5 It is about two kilometres from my home to school
6 he didn't use to ride his bike to school
7 Despite having a test tomrrow , they are still watching TV now

6 activities
2 encouragement
5 encouragement
1 invention
4 encourages
5 encouragement
à bạn ơi, bạn giải thích giùm mình chỗ mấy encouragement đc không ạ. cho mình hỏi là sao không them S vào ạ mình cảm ơn ạ


a: E thuộc Ox nên E(x;0)
O(0;0); M(4;1); E(x;0)
\(OM=\sqrt{\left(4-0\right)^2+\left(1-0\right)^2}=\sqrt{17}\)
\(OE=\sqrt{\left(x-0\right)^2+\left(0-0\right)^2}=\sqrt{x^2}=\left|x\right|\)
Để ΔOEM cân tại O thì OE=OM
=>\(\left|x\right|=\sqrt{17}\)
=>\(x=\pm\sqrt{17}\)

2.
Gọi \(H\left(x;y\right)\) là toạ độ chân đường cao ứng với BC \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}=\left(x-1;y+2\right)\\\overrightarrow{BC}=\left(2;1\right)\end{matrix}\right.\)
Do AH vuông góc BC \(\Rightarrow\overrightarrow{AH}.\overrightarrow{BC}=0\)
\(\Rightarrow2\left(x-1\right)+y+2=0\Leftrightarrow y=-2x\)
\(\Rightarrow H\left(x;-2x\right)\Rightarrow\overrightarrow{BH}=\left(x+2;-2x-3\right)\)
Do H thuộc BC nên B, C, H thẳng hàng hay các vecto \(\overrightarrow{BC};\overrightarrow{BH}\) cùng phương
\(\Rightarrow\dfrac{x+2}{2}=\dfrac{-2x-3}{1}\Rightarrow x=\dfrac{8}{5}\Rightarrow y=-\dfrac{16}{5}\) \(\Rightarrow H\left(-\dfrac{8}{5};\dfrac{16}{5}\right)\)
\(\Rightarrow\overrightarrow{AH}=\left(-\dfrac{13}{5};\dfrac{26}{5}\right)\Rightarrow\left\{{}\begin{matrix}AH=\sqrt{\left(-\dfrac{13}{5}\right)^2+\left(-\dfrac{6}{5}\right)^2}=\dfrac{13\sqrt{5}}{5}\\BC=\sqrt{2^2+1^2}=\sqrt{5}\end{matrix}\right.\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{13}{2}\)
3.
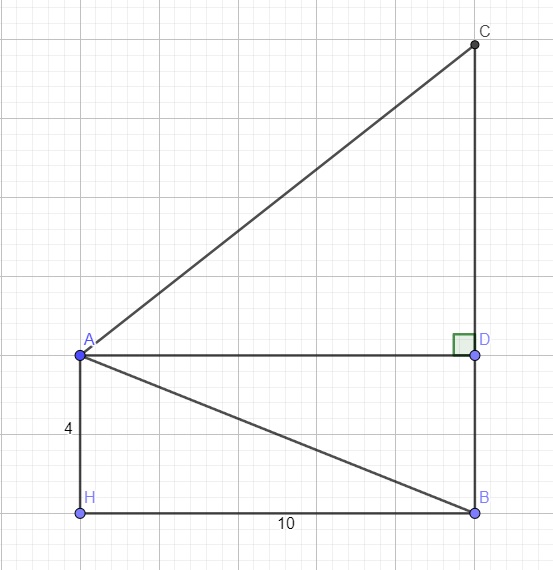
Kẻ AD vuông góc BC tại D
\(\Rightarrow AD=BH=10\) ; \(BD=AH=4\)
\(tan\widehat{BAD}=\dfrac{BD}{AD}=\dfrac{2}{5}\Rightarrow\widehat{BAD}\approx21^048'5''\)
\(\Rightarrow\widehat{CAD}=60^0-\widehat{BAD}=38^011'55''\)
\(\Rightarrow CD=AD.tan\widehat{CAD}=7,87\left(m\right)\)
\(\Rightarrow BC=BD+CD=11,87\left(m\right)\)
Câu 17:
Để (d) là hàm số bậc nhất thì \(\left\{{}\begin{matrix}a^2-4=0\\2a-4b\ne0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a^2=4\\a-2b\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\in\left\{2;-2\right\}\\b\ne\dfrac{a}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a\in\left\{2;-2\right\}\\b\notin\left\{1;-1\right\}\end{matrix}\right.\)
Câu 16:
a: Ta có: ΔOCI vuông tại C
=>\(OC^2+CI^2=OI^2\)
=>\(OC^2=6^2-\left(3\sqrt{3}\right)^2=9\)
=>\(OC=\sqrt{9}=3\left(cm\right)\)
b:
Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
Ta có: BA\(\perp\)AC
OK//BA
Do đó: OK\(\perp\)AC
Ta có: ΔOAC cân tại O
mà OI là đường cao
nên OI là phân giác của góc AOC
Xét ΔOCI và ΔOAI có
OC=OA
\(\widehat{COI}=\widehat{AOI}\)
OI chung
Do đó: ΔOCI=ΔOAI
=>\(\widehat{OCI}=\widehat{OAI}=90^0\)
=>IA là tiếp tuyến của (O)
lm hết à e