Tìm x, y thuộc Z để cho : x - y + 2xy = 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 9 2021
2.
a.
\(x^2+3x=k^2\)
\(\Leftrightarrow4x^2+12x=4k^2\)
\(\Leftrightarrow4x^2+12x+9=4k^2+9\)
\(\Leftrightarrow\left(2x+3\right)^2=\left(2k\right)^2+9\)
\(\Leftrightarrow\left(2x+3\right)^2-\left(2k\right)^2=9\)
\(\Leftrightarrow\left(2x+3-2k\right)\left(2x+3+2k\right)=9\)
| 2x+3-2k | -9 | -3 | -1 | 1 | 3 | 9 |
| 2x+3+2k | -1 | -3 | -9 | 9 | 3 | 1 |
| x | -4 | -3 | -4 | 1 | 0 | 1 |
| nhận | nhận | nhận | nhận | nhận | nhận |
Vậy \(x=\left\{-4;-3;0;1\right\}\)
b. Tương tự
\(x^2+x+6=k^2\)
\(\Leftrightarrow4x^2+4x+24=4k^2\)
\(\Leftrightarrow\left(2k\right)^2-\left(2x+1\right)^2=23\)
\(\Leftrightarrow\left(2k-2x-1\right)\left(2k+2x+1\right)=23\)
Em tự lập bảng tương tự câu trên
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 9 2021
1.
\(\Leftrightarrow x^2-2xy+y^2=-4y^2+y+1\)
\(\Leftrightarrow-4y^2+y+1=\left(x-y\right)^2\ge0\)
\(\Leftrightarrow-64y^2+16y+16\ge0\)
\(\Leftrightarrow\left(8y-1\right)^2\le17\)
\(\Rightarrow\left(8y-1\right)^2\le16\)
\(\Rightarrow-4\le8y-1\le4\)
\(\Rightarrow-\dfrac{3}{8}\le y\le\dfrac{5}{8}\)
\(\Rightarrow y=0\)
Thế vào pt ban đầu:
\(\Rightarrow x^2=1\Rightarrow x=\pm1\)
Vậy \(\left(x;y\right)=\left(-1;0\right);\left(1;0\right)\)
16 tháng 11 2017
<=> \(x=\frac{3-y}{1+2y}\)
Để x, y\(\in\)Z\(1+2y\in\text{Ư}_5\)hì \(\frac{3-y}{1+2y}\in Z\)
<=>\(3-y⋮1+2y\)
<=>\(-1-2y-5⋮1+2y\)
<=>\(1+2y\in\text{Ư}\)5
<=>\(1+2y\in\text{{}\text{ }1;-1;5;-5\)
<=>\(2y\in\text{{}0;-2;4;-6\)<=>\(y\in\text{{}0;-1;2;-3\)=>x=...
11 tháng 8 2016
Ta có: x-y+2xy=3 <=> 2x - 2y + 4xy = 6 <=> 2x.(1+2y)-2y=6 <=> 2x.(2y+1) - (2y+1) + 1 =6
<=> (2y+1).(2x-1)=5
Mà x,y thuộc Z nên 2y+1 và 2x-1 là Ư(5)
*2y+1=5,2x-1=1 => x=1, y=2
*2y+1=1; 2x-1 = 5 => x=3; y=0
*2y+1=-5; 2x-1=-1 => x=0; y=-3
*2y+1=-1; 2x-1=-5 => x=-2; y=-1
Vậy (x,y) thuộc {(1;2);(3;0); (0; -3); (-2; -1)}
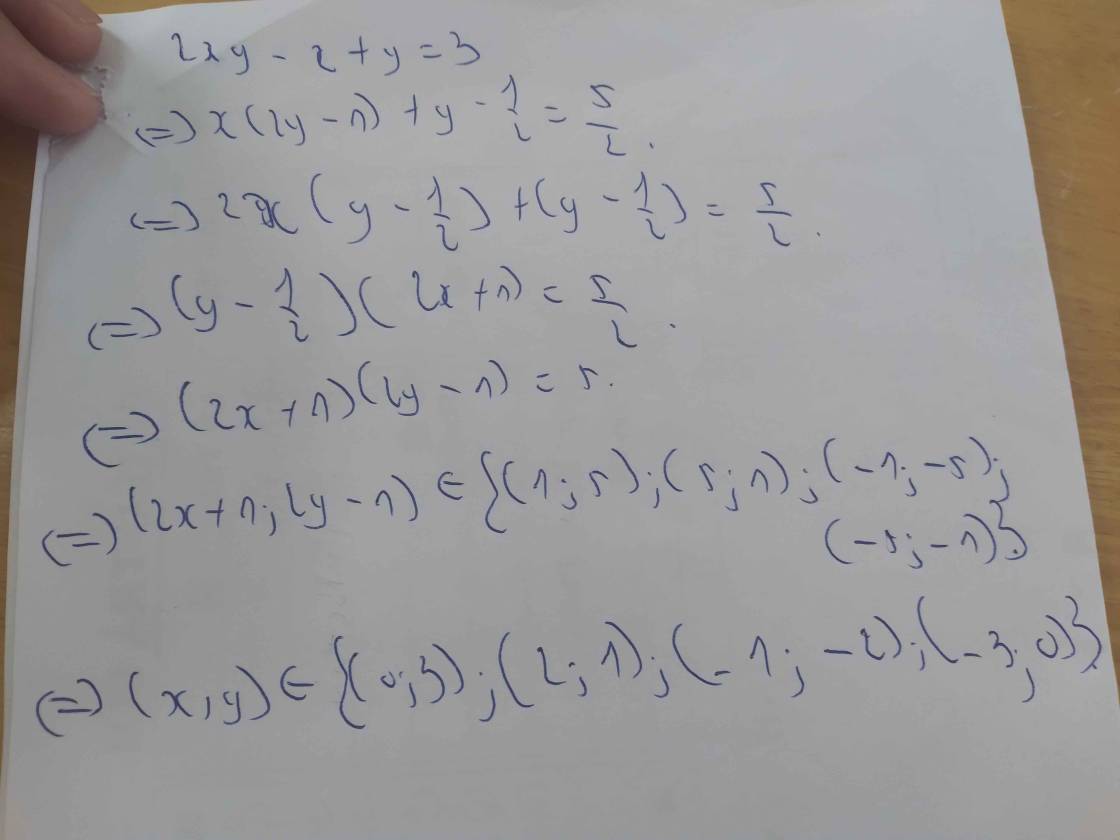
\(x-y+2xy=3\)
\(\Leftrightarrow x+2xy-y=3\)
\(\Leftrightarrow x\left(1+2y\right)-\frac{1}{2}\left(1+2y\right)+\frac{1}{2}=3\)
\(\Leftrightarrow\left(1+2y\right)\left(x-\frac{1}{2}\right)=3-\frac{1}{2}\)
\(\Leftrightarrow\left(1+2y\right)\left(x-\frac{1}{2}\right)=\frac{5}{2}\)
\(\Leftrightarrow2.\left(1+2y\right)\left(x-\frac{1}{2}\right)=\frac{5}{2}.2\) (Nhân mỗi vế với 2)
\(\Rightarrow\left(1+2y\right)\left(2x-1\right)=5\)
\(\Rightarrow1+2y\)và \(2x-1\)\(\inƯ\left(5\right)=\left\{1;5;-1;-5\right\}\)
Ta có bảng giá trị sau:
Vậy \(\left(x;y\right)\in\left\{\left(3;0\right);\left(1;2\right);\left(-2;-1\right);\left(0;-3\right)\right\}\)