Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔGAB có KC//AB
nên \(\dfrac{GC}{GB}=\dfrac{GK}{GA}\)
b: Xét ΔKAD và ΔAGB có
\(\widehat{KAD}=\widehat{AGB}\)(hai góc so le trong, DA//BC)
\(\widehat{AKD}=\widehat{GAB}\)(hai góc so le trong, DK//AB)
Do đó: ΔKAD đồng dạng với ΔAGB
=>\(\dfrac{AK}{AG}=\dfrac{AD}{GB}\)
=>\(\dfrac{AK}{AD}=\dfrac{AG}{GB}\)
=>\(\dfrac{AD}{AK}=\dfrac{BG}{GA}\)
a:
ta có: ABCD là hình bình hành
=>AB//CD
Ta có: AB//CD
K\(\in\)CD
Do đó: CK//AB
Xét ΔGAB có CK//AB
nên \(\dfrac{GC}{GB}=\dfrac{GK}{GA}\)
b:
ta có: ABCD là hình bình hành
=>BC//AD
Ta có: BC//AD
C\(\in\)BG
Do đó: BG//AD
=>\(\widehat{BGA}=\widehat{DAG}\)(hai góc so le trong)
Xét ΔBGA và ΔDAK có
\(\widehat{BGA}=\widehat{DAK}\)
\(\widehat{GBA}=\widehat{ADK}\)(ABCD là hình bình hành)
Do đó: ΔBGA đồng dạng với ΔDAK
=>\(\dfrac{BG}{DA}=\dfrac{GA}{AK}\)
=>\(\dfrac{AD}{AK}=\dfrac{BG}{GA}\)
a: Xét ΔGAB có CK//AB
nên \(\dfrac{GC}{GB}=\dfrac{GK}{GA}\)
b: Xét ΔKAD và ΔKGC có
\(\widehat{KAD}=\widehat{KGC}\)(hai góc so le trong, AD//GC)
\(\widehat{AKD}=\widehat{GKC}\)(hai góc đối đỉnh)
Do đó: ΔKAD đồng dạng với ΔKGC
=>\(\dfrac{KA}{KG}=\dfrac{AD}{GC}\)
=>\(\dfrac{KA}{AD}=\dfrac{KG}{GC}\)
=>\(\dfrac{AD}{AK}=\dfrac{GC}{GK}\)
mà \(\dfrac{GC}{GK}=\dfrac{GB}{GA}\)(GC/GB=GK/GA)
nên \(\dfrac{AD}{AK}=\dfrac{BG}{GA}\)
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔOAK và ΔOCH có
\(\widehat{OAK}=\widehat{OCH}\)(hai góc so le trong, AK//CH)
OA=OC
\(\widehat{AOK}=\widehat{COH}\)(hai góc đối đỉnh)
Do đó: ΔOAK=ΔOCH
=>OK=OH
=>O là trung điểm của KH
Xét ΔOAE và ΔOCF có
\(\widehat{EAO}=\widehat{FCO}\)(hai góc so le trong, AE//CF)
OA=OC
\(\widehat{AOE}=\widehat{COF}\)
Do đó: ΔOAE=ΔOCF
=>OE=OF
=>O là trung điểm của EF
Xét tứ giác EKFH có
O là trung điểm chung của EF và KH
=>EKFH là hình bình hành
Ta có DAOK = DCOH Þ OK =OH, DDOE = DBOF Þ OE = OF Þ EHFK là hình bình hành
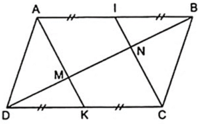
Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:
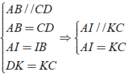
Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.
ABCD là hbh=> AD//BC=> góc DAC= góc ACB và AO=OC
Xét tam giác AOE và tam giác COF ta có
góc AOE = góc COF (2 góc đối xừng)
AO=OC
góc DAC= góc ACB
=> tam giác AOE = tam giác COF=> OE=OF
CHứng minh tương tự ta có tam giác AOK= tam giác COH=> OK=OH
Xét tứ giác EHFK có EH và FK là 2 đường chéo cắt nhau tại O
lại có OE=OF
OH=OK
=> EHFk là hình bình hành (do 2 đường chéo cắt nhau tại trung điểm mỗi đường)
bạn ghi lại đề đi bạn
sai ở đâu sao bạn