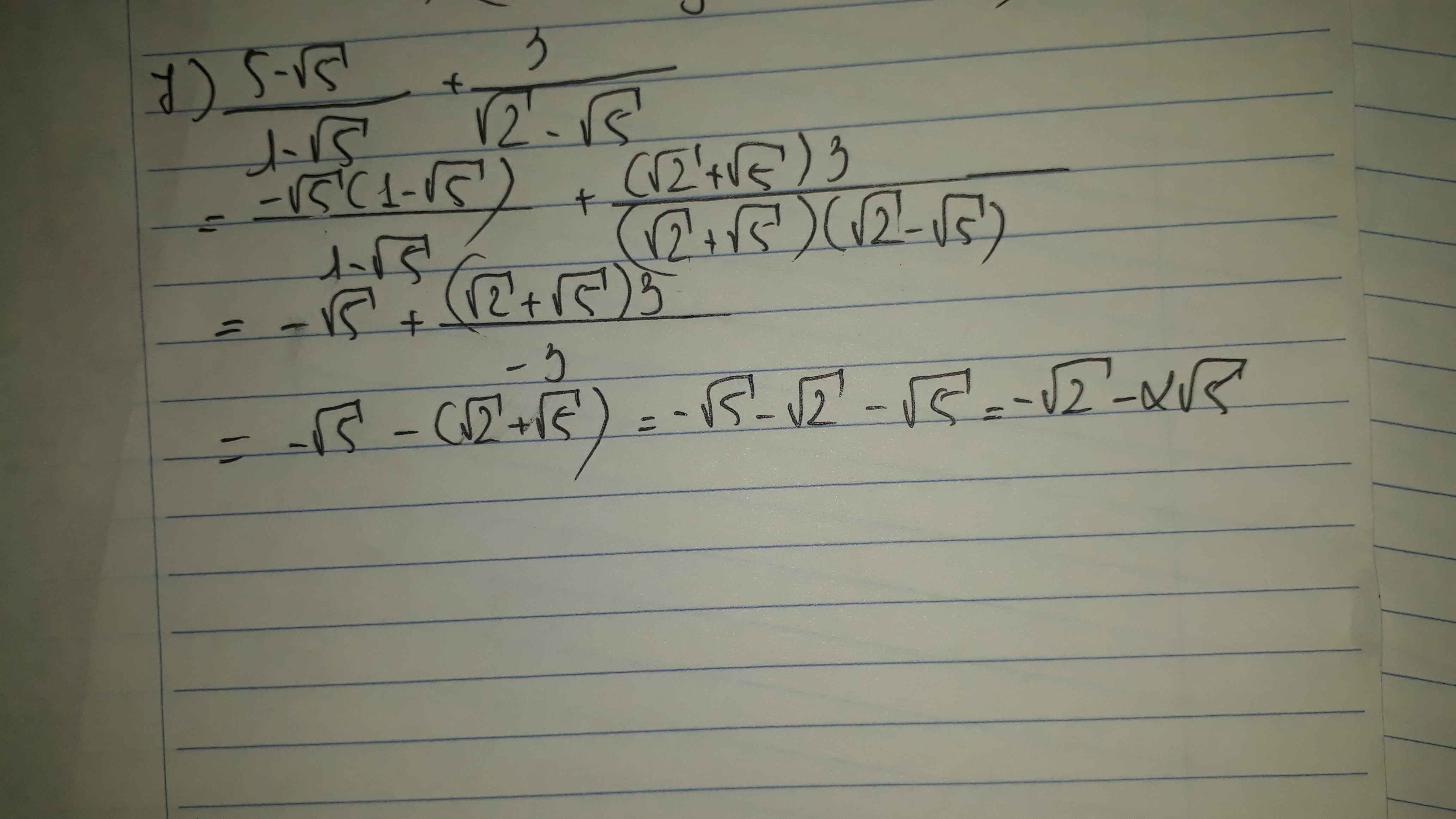giúp em câu 7 với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
L
0
SN
2
H
9 tháng 5 2021
Caai 7 :
a) C2H4 + Br2 $\to$ C2H4Br2
b) Theo PTHH : n C2H4 = n Br2 = 8/160 = 0,05(mol)
%V C2H4 = 0,05.22,4/2,24 .100% = 50%
%V CH4 = 100% -50% = 50%
H
9 tháng 5 2021
Câu 8 :
a) C2H5OH = a(mol) => n CH3COOH = 2a(mol)
$C_2H_5OH + Na \to C_2H_5OH + \dfrac{1}{2}H_2$
$CH_3COOH + Na \to CH_3COONa + \dfrac{1}{2}H_2$
Theo PTHH :
n H2 = 1/2 n C2H5OH + 1/2 n CH3COOH = 0,5a + a = 3,36/22,4 = 0,15
=> a = 0,1
=> m = 0,1.46 + 0,1.2.60 = 16,6(gam)
b)
$C_2H_5OH + CH_3COOH \buildrel{{H_2SO_4,t^o}}\over\rightleftharpoons CH_3COOC_2H_5 + H_2O$
Ta thấy : n C2H5OH < n CH3COOH nên hiệu suất tính theo số mol C2H5OH
n CH3COOC2H5 = n C2H5OH pư = 0,1.80% = 0,08(mol)
m este = 0,08.88 = 7,04(gam)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
21 tháng 11 2023
Câu 7:
Xét hình bình hành ABCD, gọi O là giao của AC và BD
\(OB=OD=\dfrac{BD}{2}\Rightarrow BD=2OB\) (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Ta có
\(BN=\dfrac{1}{3}BD\left(gt\right)\Rightarrow BN=\dfrac{1}{3}.2OB=\dfrac{2}{3}OB\)
Xét hbh ABEF, gọi I là giao của AE và BF ta có
\(IA=IE=\dfrac{AE}{2}\Rightarrow AE=2IA\) (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Ta có
\(AM=\dfrac{1}{3}AE\left(gt\right)\Rightarrow AM=\dfrac{1}{3}.2IA=\dfrac{2}{3}IA\) (1)
Xét tg ABF có
\(IB=IF\) (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường) => IA là trung tuyến của tg ABF (2)
Từ (1) và (2) => M là trọng tâm của tg ABF
Gọi K là giao của BM với AF => BK là trung tuyến của tg ABF
\(\Rightarrow BM=\dfrac{2}{3}BK\)
Xét tg BOK có
\(BN=\dfrac{2}{3}OB\left(cmt\right)\Rightarrow\dfrac{BN}{OB}=\dfrac{2}{3}\)
\(BM=\dfrac{2}{3}BK\left(cmt\right)\Rightarrow\dfrac{BM}{BK}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{BN}{OB}=\dfrac{BM}{BK}=\dfrac{2}{3}\) => MN//OK (Talet đảo trong tam giác) (3)
Xét tg ACF có
BK là trung tuyến của tg ABF (cmt) => KA=KF
Ta có
OA=OC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
=> OK là đường trung bình của tg ACF => OK//CF (4)
Từ (3) và (4) => MN//CF
mà \(CF\in\left(DCEF\right)\)
=> MN//(DCEF)
TP
21 tháng 11 2021
\(7.P_2O_5+3H_2O\rightarrow2H_3PO_4\\ n_{H_3PO_4}=2n_{P_2O_5}=0,2\left(mol\right)\\ Tacó:\dfrac{n_{KOH}}{n_{H_3PO_4}}=\dfrac{0,35}{0,2}=1,75\\ \Rightarrow Xảyracácphảnứng:\\ KOH+H_3PO_4\rightarrow KH_2PO_4+H_2O\\ 2KOH+H_3PO_4\rightarrow K_2HPO_4+2H_2O\\ Đặt:\left\{{}\begin{matrix}n_{KH_2PO_4}=x\left(mol\right)\\n_{KHPO_4}=y\left(mol\right)\end{matrix}\right.\\ Tacó:\left\{{}\begin{matrix}x+y=0,2\left(BTNT\left(P\right)\right)\\x+2y=0,35\left(BTNT\left(K\right)\right)\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x=0,05\\y=0,15\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}m_{KH_2PO_4}=6,8\left(g\right)\\m_{K_2HPO_4}=26,1\left(g\right)\end{matrix}\right.\)
HP
21 tháng 11 2021
7. \(PTHH:P_2O_5+6KOH--->2K_3PO_4+3H_2O\)
Vậy chất sau phản ứng là K3PO4
Ta thấy: \(\dfrac{0,1}{1}>\dfrac{0,35}{6}\)
Vậy P2O5 dư.
Theo PT: \(n_{K_3PO_4}=\dfrac{1}{3}.n_{KOH}=\dfrac{1}{3}.0,35=\dfrac{7}{60}\left(mol\right)\)
\(\Rightarrow m_{K_3PO_4}=\dfrac{7}{60}.212\approx24,7\left(g\right)\)
30 tháng 8 2021
7)
\(=\dfrac{\left(5-\sqrt{5}\right).\left(1+\sqrt{5}\right)}{\left(1-\sqrt{5}\right)\left(1+\sqrt{5}\right)}+\dfrac{3\left(\sqrt{2}+\sqrt{5}\right)}{\left(\sqrt{2}-\sqrt{5}\right)\left(\sqrt{2}+\sqrt{5}\right)}\)
\(=\dfrac{\left(5-\sqrt{5}\right)\left(1+\sqrt{5}\right)}{1-5}+\dfrac{3\left(\sqrt{2}+\sqrt{5}\right)}{4-5}\)
\(=\dfrac{5+5\sqrt{5}-\sqrt{5}-5}{4}+3\left(\sqrt{2}+\sqrt{5}\right)\)
=\(\dfrac{4\sqrt{5}}{4}+3\left(\sqrt{2}+\sqrt{5}\right)\)
\(=\sqrt{5}+3\sqrt{2}+3\sqrt{5}\)
\(=4\sqrt{5}+3\sqrt{2}\)
