Từ A ngoài (O), bán kính R, vẽ tiếp tuyến AE và dây EF vuông góc với OA tại M
a) cho R =10cm,OM =6cm. Tính EF
b) c/m AF là tiếp tuyến của (O)
c) kẻ đường kính EC, tiếp tuyến với (O) tại C cắt EF tại D. Tính EM.ED theo R
d) kẻ tiếp tuyến DB. c/m A,B,C thẳng hàng



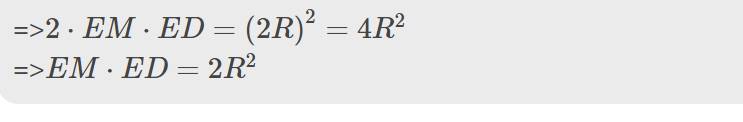
a: Xét ΔOEA vuông tại E có EM là đường cao
nên \(OM\cdot OA=OE^2\)
=>\(OA=\dfrac{10^2}{6}=\dfrac{50}{3}\left(cm\right)\)
ΔOEA vuông tại E
=>\(OE^2+EA^2=OA^2\)
=>\(EA^2+10^2=\left(\dfrac{50}{3}\right)^2\)
=>\(EA^2=\left(\dfrac{40}{3}\right)^2\)
=>EA=40/3(cm)
Xét ΔEAO vuông tại E có EM là đường cao
nên \(EM\cdot OA=EA\cdot EO\)
=>\(EM\cdot\dfrac{50}{3}=10\cdot\dfrac{40}{3}\)
=>\(EM\cdot50=10\cdot40\)
=>EM=400/50=8(cm)
Ta có: ΔOEF cân tại O
mà OM là đường cao
nên M là trung điểm của EF và OM là phân giác của góc EOF
=>\(EF=2\cdot EM=16\left(cm\right)\)
b: Xét ΔOEA và ΔOFA có
OE=OF
\(\widehat{EOA}=\widehat{FOA}\)
OA chung
Do đó: ΔOEA=ΔOFA
=>\(\widehat{OEA}=\widehat{OFA}=90^0\)
=>AFlà tiếp tuyến của (O)
c: Xét (O) có
ΔEFC nội tiếp
EC là đường kính
Do đó: ΔEFC vuông tại F
=>EF\(\perp\)FC tại F
=>CF\(\perp\)ED tại F
Xét ΔECD vuông tại C có EF là đường cao
nên \(EF\cdot ED=EC^2\)
=>\(2\cdot EM\cdot ED=\left(2R\right)^2=4R^2\)
=>\(EM\cdot ED=2R^2\)