Bài 8: Hòa tan hoàn toàn 22 gam hỗn hợp X gồm Al và Fe vào 500 ml dung dịch HCl, vừa đủ thì thu được 19,832 lít khí thoát ra (ở đkc). a. Tính thành phần phần trăm theo khối lượng mỗi kim loại trong hỗn hợp X. b. Tính nồng độ mol/lít của dung dịch HCI đã sử dụng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 12 2023
a, Ta có: 27nAl + 56nFe = 27,8 (1)
PT: \(2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\)
\(Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
Theo PT: \(n_{H_2}=\dfrac{3}{2}n_{Al}+n_{Fe}=\dfrac{17,353}{24,79}=0,7\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{Al}=0,2\left(mol\right)\\n_{Fe}=0,4\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Al}=\dfrac{0,2.27}{27,8}.100\%\approx19,42\%\\\%m_{Fe}\approx80,58\%\end{matrix}\right.\)
b, \(n_{H_2SO_4}=n_{H_2}=0,7\left(mol\right)\Rightarrow C_{M_{H_2SO_4}}=\dfrac{0,7}{0,5}=1,4\left(M\right)\)
6 tháng 3 2022
Gọi \(\left\{{}\begin{matrix}n_{Al}=x\left(mol\right)\\n_{Fe}=y\left(mol\right)\end{matrix}\right.\)
\(n_{H_2}=\dfrac{4,48}{22,4}=0,2mol\)
\(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
\(Fe+2HCl\rightarrow FeCl_2+H_2\)
Theo pt: \(\Rightarrow\left\{{}\begin{matrix}3x+y=0,2\\27x+56y=5,5\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{19}{470}\\y=\dfrac{37}{470}\end{matrix}\right.\)
\(\%m_{Al}=\dfrac{\dfrac{19}{470}\cdot27}{5,5}\cdot100\%=19,84\%\)
\(\%m_{Fe}=100\%-19,84\%=80,16\%\)
17 tháng 3 2021
a) Đặt \(\left\{{}\begin{matrix}n_{Mg}=a\left(mol\right)\\n_{Al}=b\left(mol\right)\end{matrix}\right.\) \(\Rightarrow24a+27b=5,1\) (1)
Ta có: \(n_{H_2}=\dfrac{5,6}{22,4}=0,25\left(mol\right)\)
Bảo toàn electron: \(2a+3b=0,5\) (2)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}a=0,1\\b=0,1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Mg}=\dfrac{0,1\cdot24}{5,1}\cdot100\%\approx47,06\%\\\%m_{Al}=52,94\%\end{matrix}\right.\)
b) Bảo toàn nguyên tố: \(n_{HCl}=2n_{H_2}=0,5\left(mol\right)\)
\(\Rightarrow m_{ddHCl}=\dfrac{0,5\cdot36,5}{7,3\%}=250\left(g\right)\)
\(\Rightarrow V_{HCl}=\dfrac{250}{1,2}\approx208,33\left(ml\right)\)
14 tháng 2 2022
a) Gọi số mol Zn, Fe là a, b (mol)
=> 65a + 56b = 8,56 (1)
\(n_{H_2}=\dfrac{3,136}{22,4}=0,14\left(mol\right)\)
PTHH: Zn + 2HCl --> ZnCl2 + H2
a--->2a-------->a----->a
Fe + 2HCl --> FeCl2 + H2
b----->2b------->b------>b
=> a + b = 0,14 (2)
(1)(2) => a = 0,08; b = 0,06
=> \(\left\{{}\begin{matrix}\%m_{Zn}=\dfrac{0,08.65}{8,56}.100\%=60,748\%\\\%m_{Fe}=\dfrac{0,06.56}{8,56}.100\%=39,252\%\end{matrix}\right.\)
b)
nKOH = 0,2.0,1 = 0,02 (mol)
PTHH: KOH + HCl --> KCl + H2O
0,02-->0,02
=> nHCl = 0,02 + 2a + 2b = 0,3 (mol)
=> \(C_{M\left(HCl\right)}=xM=\dfrac{0,3}{0,15}=2M\)
c) m = 0,08.136 + 0,06.127 = 18,5(g)
TP
1 tháng 9 2021
\(a)2Al+HCl\rightarrow2AlCl_3+3H_2\\ Fe+2HCl\rightarrow FeCl_2+H_2\)
b) \(n_{HCl}=\dfrac{8,96}{22,4}=0,4\left(mol\right)\\ Gọi:n_{Al}=x\left(mol\right);n_{Fe}=y\left(mol\right)\\ Tacó:\left\{{}\begin{matrix}27x+56y=m_{hh}\\\dfrac{3}{2}x+y=0,4\end{matrix}\right.\)
Đề thiếu dữ kiện, xem lại đề nha bạn !
9 tháng 3 2023
Gọi: \(\left\{{}\begin{matrix}n_{Al}=x\left(mol\right)\\n_{Fe}=y\left(mol\right)\end{matrix}\right.\) ⇒ 27x + 56y = 5,5 (1)
PT: \(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
\(Fe+2HCl\rightarrow FeCl_2+H_2\)
Theo PT: \(n_{H_2}=\dfrac{3}{2}n_{Al}+n_{Fe}=\dfrac{3}{2}x+y=\dfrac{4,48}{22,4}=0,2\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}x=0,1\left(mol\right)\\y=0,05\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Al}=\dfrac{0,1.27}{5,5}.100\%\approx49,09\%\\\%m_{Fe}\approx50,91\%\end{matrix}\right.\)
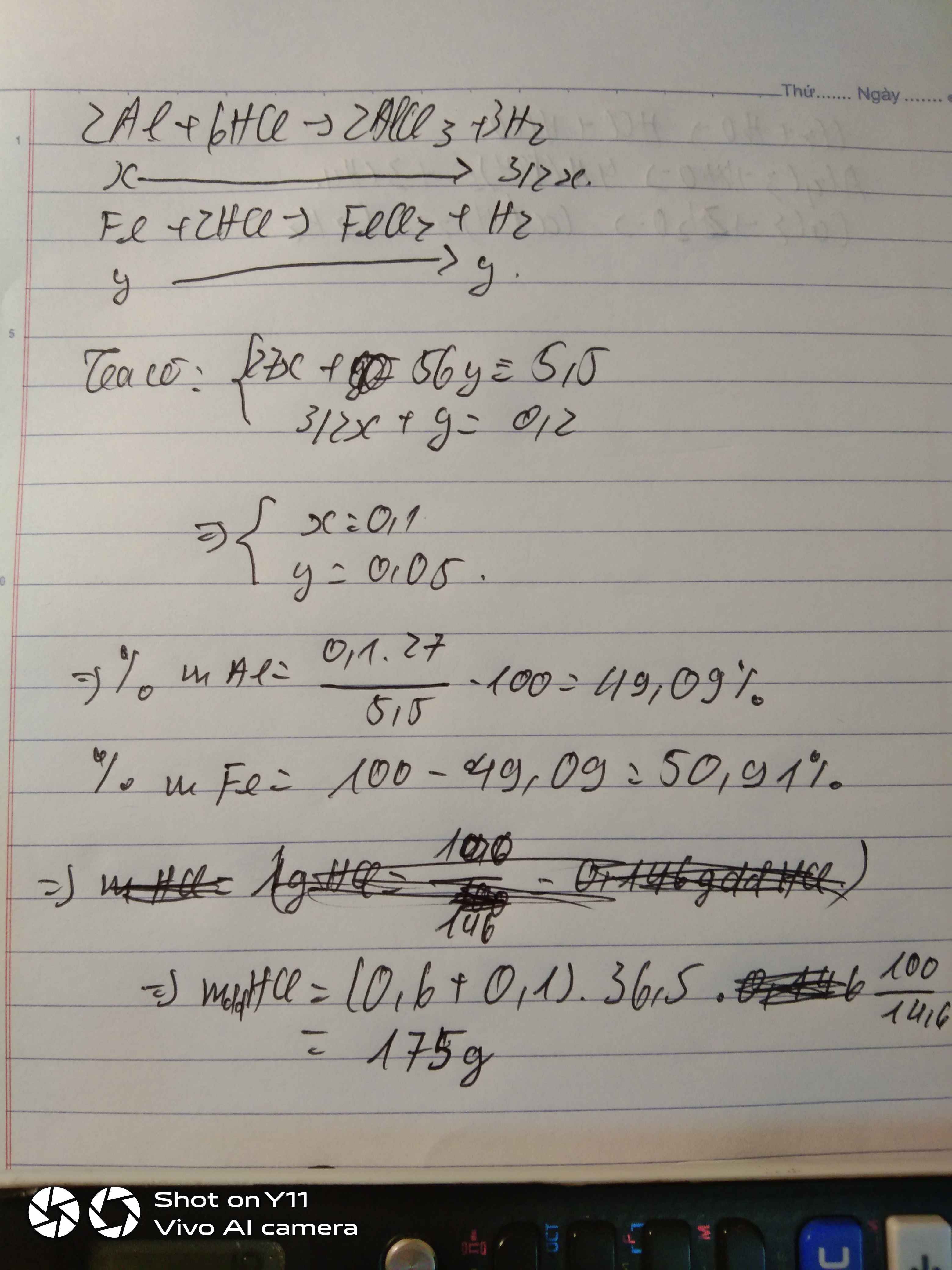
a, Ta có: 27nAl + 56nFe = 22 (1)
PT: \(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
\(Fe+2HCl\rightarrow FeCl_2+H_2\)
Theo PT: \(n_{H_2}=\dfrac{3}{2}n_{Al}+n_{Fe}=\dfrac{19,832}{24,79}=0,8\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}m_{Al}=0,4\left(mol\right)\\n_{Fe}=0,2\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Al}=\dfrac{0,4.27}{22}.100\%\approx49,09\%\\\%m_{Fe}\approx50,91\%\end{matrix}\right.\)
b, \(n_{HCl}=2n_{H_2}=1,6\left(mol\right)\)
\(\Rightarrow C_{M_{HCl}}=\dfrac{1,6}{0,5}=3,2\left(M\right)\)