Cho đường thẳng xx' cắt yy' tại A; biết góc xAy = 36 độ. Vẽ tia phân giác At của góc xAy và tia phân giác At' của x'Ay'. Chứng minh rằng: góc xAt và góc x'At' là 2 góc đối đỉnh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Nếu tia At không cắt yy'
=> At // yy'
=> At trung với Ax (vì xx' // yy')
Mà At là phân giác góc xAb
=> At nằm giữa Ax và AB
=> At không trùng Ax
=> At cắt yy'
b,
Bạn xem lại đề. C ở đâu vậy?

x A y C t B x y
Câu a ta có :
At > yy (gt)
mà xx /yy (gt)
At yy ( hệ quả tiền đề Ô =lít)
câu b:
Vì AT tia phân giác xAb
=> xAt = =BaT =40 độ
Vậy :
bCE>BEC
~Study well~

a, Nếu tia At không cắt yy'
=> At // yy'
=> At trung với Ax (vì xx' // yy')
Mà At là phân giác góc xAb
=> At nằm giữa Ax và AB
=> At không trùng Ax
=> At cắt yy'
b,
Bạn xem lại đề. C ở đâu vậy?

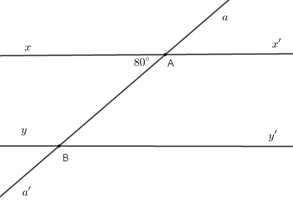
a, Ta có: At∩xx′={A}(gt)At∩xx′={A}(gt)
Mà xx' // yy' (gt)
=> At ∩∩ yy' (hệ quả của tiên đề ơ-clit)
b,Tia At là phân giác góc xAB (gt)
=> góc xAt = góc BAt = Góc xAB / 2 = 80o/2 = 40o
Có: xx' // yy' (gt)
mà At ∩∩ yy' = {C} (gt)
=> Góc xAt = góc ACB = 40o (cặp góc so le trong )

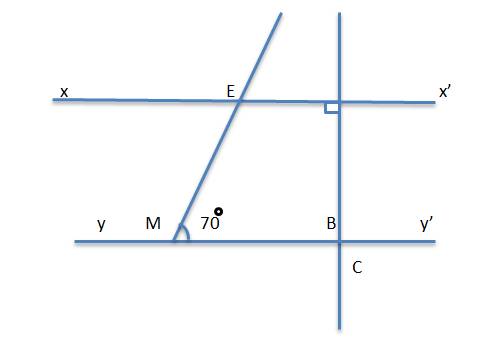
a) Ta có:
\(xx'\perp C\left(gt\right)\)
\(yy'\perp C\left(gt\right)\)
\(\Rightarrow xx'//yy'\)
b) Ta có: \(xx'//yy'\) và tia \(Mz\) cắt \(xx'\) nên:
\(\widehat{xEM}=\widehat{EMB}\) (so le trong)
\(\Rightarrow\widehat{xEM}=70^o\)
Mà: \(\widehat{xEM}\) đối đỉnh với \(\widehat{zEA}\) nên:
\(\Rightarrow\widehat{zEA}=\widehat{xEM}=70^o\)
\(\widehat{xEz}+\widehat{zEA}=180^o\) (kề bù)
\(\Rightarrow\widehat{xEz}=180^o-70^o=110^o\)
\(\widehat{MEA}+\widehat{xEM}=180^o\) (kề bù)
\(\Rightarrow\widehat{MEA}=180^o-70^o=110^o\)

\(AC//BD\Rightarrow\widehat{CAM}=\widehat{DBM}\)
\(M\)trung điểm \(AB\Rightarrow AM=BM\)
\(\widehat{CMA}=\widehat{DMB}\)(2 góc đối đỉnh)
\(\Rightarrow\Delta CAM=\Delta DBM\left(g.c.g\right)\Rightarrow AC=BD\)
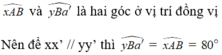
Ta có: góc xAt= 1/2 góc xAy; góc x'At' =1/2 góc x'Ay'
mà góc xAy = x'At' ( hai góc đối đỉnh)
=> xAt=x'At'
Ta có xAy+ yAx' = 180
=> 36* + yAx' = 180
=> yAx' = 144
Ta có tAt' = tAy + yAx' +t'Ax'
= 1/2 xAy + 144 + 1/2 x'Ay'
mà xAy = x'Ay' (đối đỉnh)
=> tat' = 1/2. 36 + 144+ 1/2 . 36
= 180
=> t, A, t' thẳng hàng
mà xAt = x'At' (cmt)
=> điều phải chứng minh.
b, Ta có:
xOtˆ=x′Ot′ˆ;yOtˆ=y′Ot′ˆxOt^=x′Ot′^;yOt^=y′Ot′^
mà xOtˆ=yOtˆ(gt)xOt^=yOt^(gt)
nên x′Ot′ˆ=y′Ot′ˆx′Ot′^=y′Ot′^
=> Ot' là phân giác của x′Oy′ˆx′Oy′^.(đpcm)