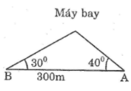
Câu 3. Hai người đứng ở vị trí A và B quan sát một máy bay trực thăng đang ở vị trí C với các góc lần lượt là 45° và 30° (như hình vẽ (bên dưới). Biết máy bay cách vị trí B là 260m. tính khoảng cách từ máy bay đến vị trị A
Câu 4. Cho đường tròn (O) đường kính AB = 2R. Trên đường tròn (O) lấy điểm C (C khác A, khác B) sao cho CA < CB. Tiếp tuyến tại A của đường tròn (O) cắt BC tại E
a) Chứng minh tam giác ABC vuông và BC.BE=4R2
b) Đường thẳng qua A vuông góc với OE tại I và cắt đường tròn (O) tại D. Chứng minh bồn điểm A, E,C,I cùng thuộc một đường tròn.
c) Chứng minh ED là tiếp tuyến của đường tròn (O) và góc ECD = góc EDB

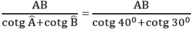 ≈ 102,606 (cm)
≈ 102,606 (cm)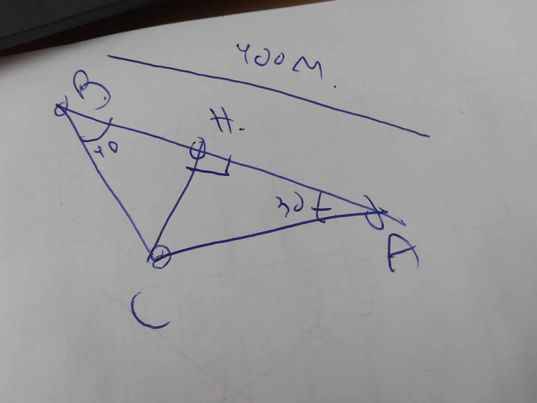

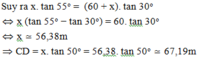
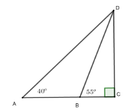

Câu 3:
Xét ΔCAB có \(\dfrac{CB}{sinA}=\dfrac{CA}{sinB}\)
=>\(\dfrac{260}{sin45}=\dfrac{CA}{sin30}\)
=>\(CA\simeq183,85\left(m\right)\)
Câu 4:
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
=>AC\(\perp\)CB tại C
=>AC\(\perp\)EB tại C
Xét ΔABE vuông tại A có AC là đường cao
nên \(BC\cdot BE=BA^2=\left(2R\right)^2=4R^2\)
b: Ta có: ΔOAD cân tại O
mà OE là đường cao
nên OE là phân giác của góc AOD
Xét ΔOAE và ΔODE có
OA=OD
\(\widehat{AOE}=\widehat{DOE}\)
OE chung
Do đó: ΔOAE=ΔODE
=>\(\widehat{OAE}=\widehat{ODE}=90^0\)
Xét tứ giác EAOD có
\(\widehat{EAO}+\widehat{EDO}=90^0+90^0=180^0\)
=>EAOD là tứ giác nội tiếp
=>E,A,O,D cùng thuộc một đường tròn
c: Xét (O) có
OD là bán kính
ED\(\perp\)DO tại D
Do đó: ED là tiếp tuyến của (O)
Xét (O) có
\(\widehat{EDC}\) là góc tạo bởi tiếp tuyến DE và dây cung DC
\(\widehat{CBD}\) là góc nội tiếp chắn cung DC
Do đó: \(\widehat{EDC}=\widehat{CBD}\)
=>\(\widehat{EDC}=\widehat{EBD}\)
Xét ΔEDC và ΔEBD có
\(\widehat{EDC}=\widehat{EBD}\)
\(\widehat{DEC}\) chung
Do đó: ΔEDC đồng dạng với ΔEBD
=>\(\widehat{ECD}=\widehat{EDB}\)