Cho đường tron (O) đường kính AB, một điểm M di động trên đường tròn. Gọi N là điểm đối xứng vs A wa M,P là giao điểm thứ hai của đường BN với đường tròn (O); Q,R là giao điểm của đường thẳng BM lần lượt với AP và tiếp tuyến tại A của đường tròn (O).
a) CMR N luôn luôn nằm trên đường tròn cố định tiếp xúc với đường tròn (O. Gọi đó là đường tròn (C)
b) CM RN là tiếp tuyến của đường tròn (C)
c) Tứ giác ARNQ là hình gì? Tại sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Tam giác AMB nội tiếp đường tròn (O) có AB là đường kính nên là tam giác vuông.
=> \(AM\perp MB\)
N và B đối xứng qua M nên MN = MB
+) Tam giác NAB có AM vừa là đường cao vừa là trung tuyến nên là tam giác cân.
=> AN = AB = không đổi
Vậy khi M di động trên đường tròn (O) thì N di động trên đường tròn (A; AB)
Ta lại có: AO là đường nối tâm, AB là bán kính đường tròn (A), OB là bán kính đường tròn (O).
Mà AO = AB - OB
Vậy đường tròn (O; OB) tiếp xúc đường tròn (A; AB) tại B.

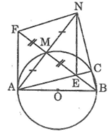
Ta có: MA = MN (tính chất đối xứng tâm)
ME = MF (tính chất đối xứng tâm)
Tứ giác AENF có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
Suy ra: AF // NE
Mà NE ⊥ AB (chứng minh trên)
Suy ra: AF ⊥ AB tại A
Vậy FA là tiếp tuyến của đường tròn (O).

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xet ΔNAB có
AC.BM là các đường cao
AC cắt BM tại E
Do đó: E là trực tâm
=>NE vuông góc với AB
b: Xét tứ giác NEAF có
M là trung điểm chung của NA và EF
nên NEAF là hình bình hành
=>NE//AF
=>AF vuông góc với AB
=>FA là tiêp tuyến của (O)

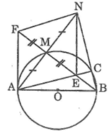
Tam giác ABM nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại M
Suy ra: AN ⊥ BM
Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại C
Suy ra: AC ⊥ BN
Tam giác ABN có hai đường cao AC và BM cắt nhau tại E nên E là trực tâm của tam giác ABN
Suy ra: NE ⊥ AB

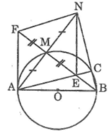
Trong tam giác ABN ta có: AN ⊥ BM và AM = MN
Suy ra tam giác ABN cân tại B
Suy ra BA = BN hay N thuộc đường tròn (B; BA)
Tứ giác AFNE là hình bình hành nên AE // FN hay FN // AC
Mặt khác: AC ⊥ BN (chứng minh trên)
Suy ra: FN ⊥ BN tại N
Vậy FN là tiếp tuyến của đường tròn (B; BA)
