Có ai biết không giúp mình với
Chứng minh rằng nếu a/b < c/d thì a/b < a+c/b+d < c/d
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


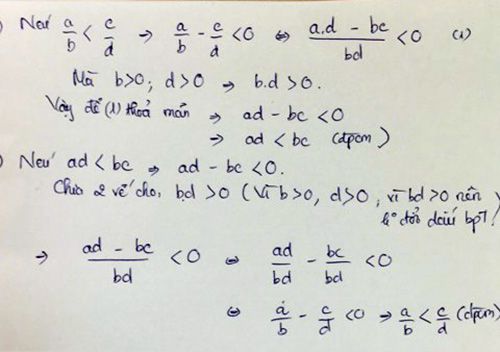
Làm nhắn gọn hơn thì
1
a/b < c/d
=> ad/bd < cb/db
=> ad < cb
2
ad < cb
=>ad /bd < cb/bd
Chúc pn hc tốt

Bài làm
- Xét a(b+2001)=ab+2001a
b(a+2001)=ab+2001b
- Ta xét 3 trường hợp sau:
+Nếu a>b =>2001a>2001b
=>a(b+2001)>b+(a+2001)
=>a/b > a+2001/b+2001
+Nếu a<b =>2001a<2001b
=>a(b+2001)<b+(a+2001)
=>a/b < a+2001/b+2001
+Nếu a=b =>a/b = a+2001/b+2001
a, Ta có: \(\hept{\begin{cases}\frac{a}{b}=\frac{ad}{bd}\\\frac{c}{d}=\frac{bc}{bd}\end{cases}}\)
Mà \(\frac{a}{b}< \frac{c}{d}\Rightarrow\frac{ad}{bd}< \frac{bc}{bd}\Rightarrow ad< bc\)
b, Ta có: \(ad< bc\Rightarrow\frac{ad}{bd}< \frac{bc}{bd}\Rightarrow\frac{a}{b}< \frac{c}{d}\)

a) \(\frac{a}{b}< \frac{c}{d}\)\(\Rightarrow\frac{ad}{bc}< \frac{bc}{bd}\)\(\Rightarrow ad< bc\)
b) ad < bc \(\Rightarrow\frac{ad}{bd}< \frac{bc}{bd}\)( vì bd > 0 )\(\Rightarrow\frac{a}{b}< \frac{c}{d}\)
a) Ta có: \(\hept{\begin{cases}\frac{a}{b}=\frac{ad}{bd}\\\frac{c}{d}=\frac{cb}{db}\end{cases}}\)
Mà \(\frac{a}{b}< \frac{c}{d}\Rightarrow\frac{ad}{bd}< \frac{cb}{bd}\Rightarrow ad< cb\)
b) Nếu \(ad< bc\Rightarrow\frac{ad}{bd}< \frac{bc}{bd}\Rightarrow\frac{a}{b}< \frac{c}{d}\)

a) a/b=ad/bd
c/d=cb/db
mà a/b<c/d=>ad/bd<cb/bd=>ad<bc
b)ad<bc=>ad/bd<bc/bd=> a/b<c/d

*\(\frac{a}{b}<\frac{a+c}{b+d}\)=>ab+ad<ab+bc(b,d thuộc N*)
=>ad<bc
Nhân cả hai vế cho 1/bd ta được:
a/b < c/d(Đúng với giả thiết) (b,d thuộc N*)
=>\(\frac{a}{b}<\frac{a+c}{b+d}\)
*\(\frac{a+c}{b+d}<\frac{c}{d}\)=>ad+cd<bc+cd (b,d thuộc N*)
=>ad<bc
Nhân cả hai vế cho 1/bd ta được:
=>a/b<c/d (đúng với giả thiết) (b,d thuộc N*)
Vậy \(\frac{a}{b}<\frac{a+c}{b+d}<\frac{c}{d}\)

Ta có : \(\frac{a}{b}<\frac{c}{d}\Rightarrow\frac{ad}{bd}<\frac{cb}{bd}\)
\(\Rightarrow\)\(ad\)\(<\)\(cb\) (vì \(bd>0\)) \(\left(1\right)\)
\(\frac{a}{b}=\frac{a\left(b+d\right)}{b\left(b+d\right)}=\frac{ab+ad}{b\left(b+d\right)}\)
\(\frac{a+c}{b+d}=\frac{\left(a+c\right)b}{\left(b+d\right)b}=\frac{ab+cb}{b\left(b+d\right)}\)
vì \(b,d>0\Rightarrow b\left(b+d\right)>0\) \(\left(1\right)\)
vì \(ad\)\(<\)\(cd\Rightarrow\)\(ab+ad\)\(<\)\(ab+cb\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\) \(\frac{ab+ad}{b\left(b+d\right)}<\frac{ab+cb}{b\left(b+d\right)}\)
hay \(\frac{a}{b}<\frac{a+c}{b+d}\) \(\left(\cdot\right)\)
\(\frac{a+c}{b+d}=\frac{d\left(a+c\right)}{d\left(b+d\right)}=\frac{ad+cd}{d\left(b+d\right)}\)
\(\frac{c}{d}=\frac{c\left(b+d\right)}{d\left(b+d\right)}=\frac{cb+cd}{d\left(b+d\right)}\)
Vì \(ad\)\(<\)\(cd\Rightarrow\)\(ad+cd<\)\(cb+cd\) \(\left(3\right)\)
Từ \(\left(1\right)\) và \(\left(3\right)\) \(\Rightarrow\frac{ad+cd}{d\left(b+d\right)}<\frac{cb+cd}{d\left(b+d\right)}\)
hay \(\frac{a+c}{b+d}<\frac{c}{d}\) \(\left(\cdot\cdot\right)\)
Từ \(\left(\cdot\right)\) và \(\left(\cdot\cdot\right)\Rightarrow\frac{a}{b}<\frac{a+c}{b+d}<\frac{c}{d}\)