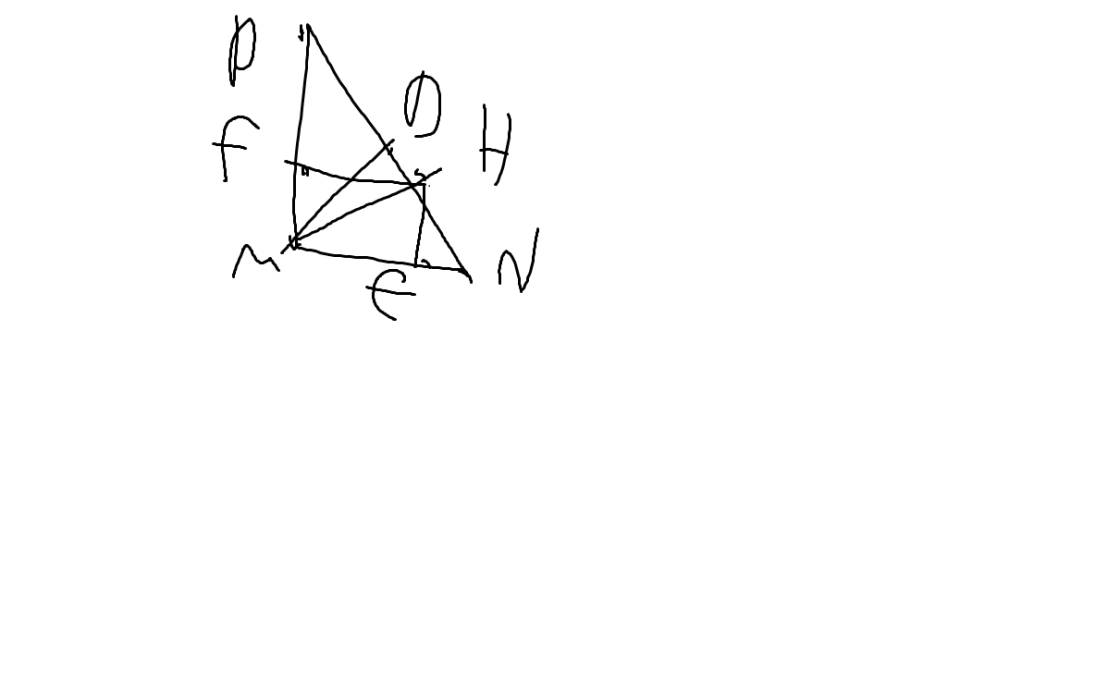vẽ hình nx nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 12 2023
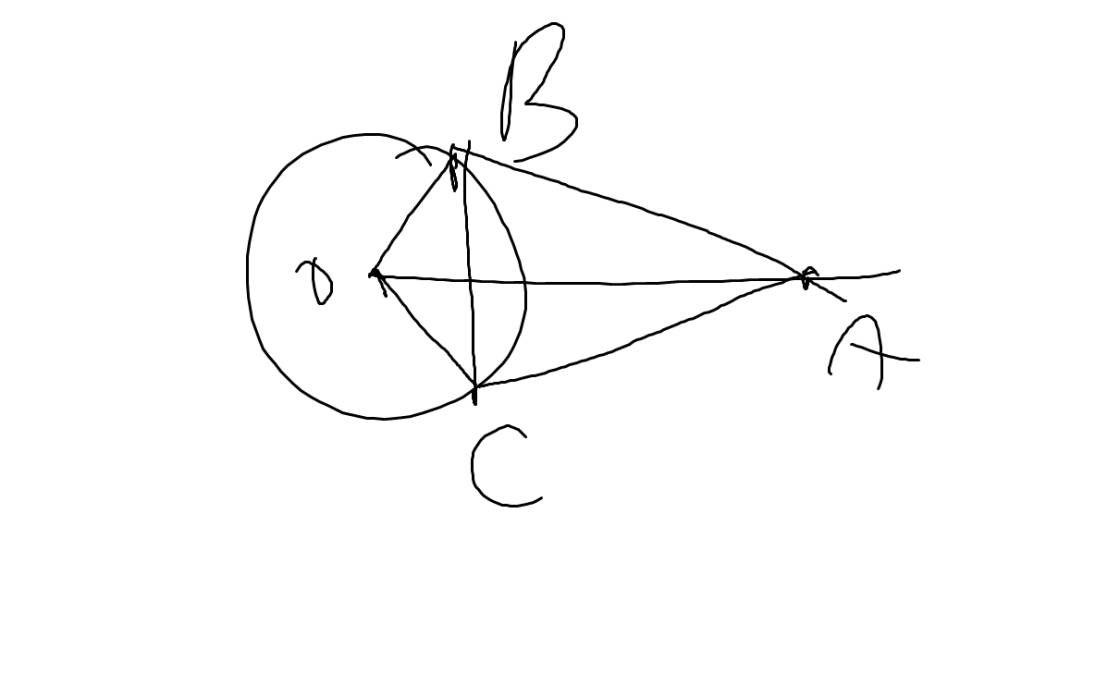
1: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
2: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại trung điểm của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔABO vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(3\right)\)
Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
=>BE\(\perp\)ED tại E
=>BE\(\perp\)AD tại E
Xét ΔDBA vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\left(4\right)\)
Từ (3) và (4) suy ra \(AE\cdot AD=AH\cdot AO\)
3: Xét ΔOKA vuông tại K và ΔOHF vuông tại H có
\(\widehat{KOA}\) chung
Do đó: ΔOKA đồng dạng với ΔOHF
=>\(\dfrac{OK}{OH}=\dfrac{OA}{OF}\)
=>\(OH\cdot OA=OK\cdot OF\left(5\right)\)
Xét ΔOCA vuông tại C có CH là đường cao
nên \(OH\cdot OA=OC^2=OD^2\left(6\right)\)
Từ (5) và (6) suy ra \(OK\cdot OF=OD^2\)
=>\(\dfrac{OK}{OD}=\dfrac{OD}{OF}\)
Xét ΔOKD và ΔODF có
\(\dfrac{OK}{OD}=\dfrac{OD}{OF}\)
\(\widehat{KOD}\) chung
Do đó: ΔOKD đồng dạng với ΔODF
=>\(\widehat{ODF}=\widehat{OKD}=90^0\)
=>FD là tiếp tuyến của (O;R)
vẽ hình nx nha
14 tháng 12 2023
a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của BA(1)
Ta có: OB=OA
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại H và H là trung điểm của AB
b: Xét (O) có
ΔADE nội tiếp
AE là đường kính
Do đó: ΔADE vuông tại D
=>AD\(\perp\)DE tại D
=>AD\(\perp\)EM tại D
Xét ΔAEM vuông tại A có AD là đường cao
nên \(MD\cdot ME=MA^2\left(3\right)\)
Xét ΔMOA vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MD\cdot ME=MH\cdot MO\)
c: Ta có: ΔOED cân tại O
mà OF là đường trung tuyến
nên OF\(\perp\)ED tại F
Xét ΔOFM vuông tại F và ΔOHK vuông tại H có
\(\widehat{HOK}\) chung
Do đó: ΔOFM đồng dạng với ΔOHK
=>\(\dfrac{OF}{OH}=\dfrac{OM}{OK}\)
=>\(OF\cdot OK=OH\cdot OM\left(5\right)\)
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2=OD^2\left(6\right)\)
Từ (5) và (6) suy ra \(OF\cdot OK=OD^2\)
=>\(\dfrac{OF}{OD}=\dfrac{OD}{OK}\)
Xét ΔOFD và ΔODK có
\(\dfrac{OF}{OD}=\dfrac{OD}{OK}\)
\(\widehat{FOD}\) chung
Do đó: ΔOFD đồng dạng với ΔODK
=>\(\widehat{OFD}=\widehat{ODK}=90^0\)
=>KD là tiếp tuyến của (O)
vẽ hình nx nha
14 tháng 12 2023
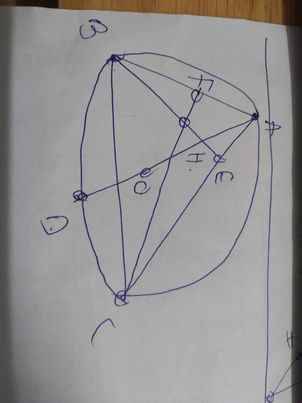
a: Xét (O) có
MA,MC là các tiếp tuyến
Do đó: MA=MC
=>M nằm trên đường trung trực của AC(1)
Ta có: OA=OC
=>O nằm trên đường trung trực của AC(2)
Từ (1) và (2) suy ra MO là đường trung trực của AC
=>MO\(\perp\)AC tại H và H là trung điểm của AC
Xét tứ giác MAOC có
\(\widehat{MAO}+\widehat{MCO}=90^0+90^0=180^0\)
=>MAOC là tứ giác nội tiếp
=>M,A,O,C cùng thuộc một đường tròn
b: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>AD\(\perp\)DB tại D
=>AD\(\perp\)MB tại D
Xét ΔMAB vuông tại A có AD là đường cao
nên \(MD\cdot MB=MA^2\left(3\right)\)
Xét ΔMAO vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MD\cdot MB=MH\cdot MO\)
21 tháng 12 2023
a: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
=>BFEC là tứ giác nội tiếp
=>B,F,E,C cùng thuộc một đường tròn
vẽ hình giúp mik nx nha
14 tháng 12 2023
a: Xét tứ giác BCEF có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
=>BCEF là tứ giác nội tiếp
=>B,C,E,F cùng thuộc một đường tròn
b: Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
=>AEHF là tứ giác nội tiếp
=>A,E,H,F cùng thuộc một đường tròn
c: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB đồng dạng với ΔAFC
=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
=>\(AE\cdot AC=AB\cdot AF\)
d: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>AB\(\perp\)BD
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD
Ta có: BE\(\perp\)AC
CD\(\perp\)CA
Do đó: BE//CD
=>BH//CD
Ta có: CH\(\perp\)AB
BD\(\perp\)AB
Do đó: CH//BD
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HD
Xét ΔDAH có
M,O lần lượt là trung điểm của DH,DA
=>MO là đường trung bình của ΔDAH
=>MO=AH/2
=>AH=2MO
LT
1
11 tháng 11 2023
a: AB và AC là hai tiếp tuyến cắt nhau tại A
b: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>OBAC là tứ giác nội tiếp
=>O,B,A,C cùng thuộc 1 đường tròn
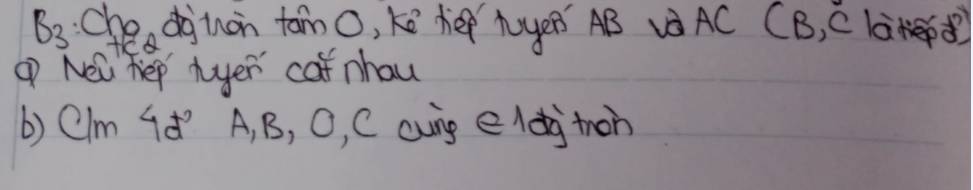
Vẽ e hình nx nhé
