Câu 24/Đề 1:Cho đồ thị (C):y=x3-3x2+1. Tiếp tuyến của (C) tại điểm có hoành độ bằng 3 tạo với hai trục toạ độ thành một tam giác có diện tích bằng:
A.234
B.117
C.\(\dfrac{238}{9}\)
D.\(\dfrac{338}{9}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
y ' = 3 x 2 + 6 x ;
Phương trình tiếp tuyến của (C) tại điểm x 0 = 0 là Δ : y = − 1 .
Giao điểm của (C) và Δ là nghiệm của hệ phương trình
y = − 1 y = x 3 + 3 x 2 − 1 ⇔ x 3 + 3 x 2 − 1 = − 1 y = − 1 ⇔ x = 0 x = − 3 y = − 1
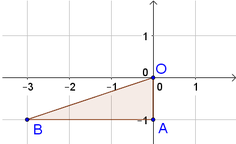
Do đó giao điểm B − 3 ; − 1 .
Tam giác OAB vuông tại A nên S O A B = 1 2 . O A . A B = 1 2 .1.3 = 3 2 .

\(y'=\dfrac{-4}{\left(x-1\right)^2}\)
a) \(y'=-1\Rightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
pt tiếp tuyến : \(\left[{}\begin{matrix}y=-\left(x-3\right)+4=-x+7\\y=-\left(x+1\right)=-x-1\end{matrix}\right.\)
b) \(k=\pm1\)
\(y'< 0\forall x\Rightarrow y'=-1\)
làm như trên
c) hoành độ tiếp điểm \(x=\pm2\)
TH x = 2
\(k=-4\)
pt tiếp tuyến : \(y=-4\left(x-2\right)+6=-4x+14\)
TH x = -2
\(k=-\dfrac{4}{9}\)
pt tiếp tuyến : \(y=-\dfrac{4}{9}\left(x+2\right)+\dfrac{2}{3}=-\dfrac{4}{9}x-\dfrac{2}{9}\)

\(y'=\dfrac{-3-m}{\left(x-1\right)^2}\) ; \(y\left(2\right)=m+5\) ; \(y'\left(2\right)=-m-3\)
Phương trình tiếp tuyến tại điểm có hoành độ \(x=2\):
\(y=\left(-m-3\right)\left(x-2\right)+m+5\)
\(\Leftrightarrow y=-\left(m+3\right)x+3m+11\)
Để tiếp tuyến cắt 2 trục tạo thành tam giác \(\Rightarrow m\ne\left\{-3;-\dfrac{11}{3}\right\}\)
Gọi A và B lần lượt là giao điểm của tiếp tuyến với Ox và Oy
\(\Rightarrow A\left(\dfrac{3m+11}{m+3};0\right)\) ; \(B\left(0;3m+11\right)\)
\(\Rightarrow OA=\left|\dfrac{3m+11}{m+3}\right|\) ; \(OB=\left|3m+11\right|\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{25}{2}\Rightarrow\dfrac{\left(3m+11\right)^2}{\left|m+3\right|}=25\)
\(\Leftrightarrow\left(3m+11\right)^2=25\left|m+3\right|\Rightarrow\left[{}\begin{matrix}\left(3m+11\right)^2=-25\left(m+3\right)\\\left(3m+11\right)^2=25\left(m+3\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}9m^2+91m+196=0\\9m^2+41m+46=0\end{matrix}\right.\) \(\Rightarrow m=...\)
(C): \(y=x^3-3x^2+1\)
=>\(y'=3x^2-3\cdot2x=3x^2-6x\)
Tiếp tuyến của (C) tại điểm có x=3 có dạng là:
\(y-y\left(3\right)=f'\left(3\right)\cdot\left(x-3\right)\)
=>\(y-\left(3^3-3\cdot3^2+1\right)=\left(3\cdot3^2-6\cdot3\right)\left(x-3\right)\)
=>\(y-1=9\left(x-3\right)=9x-27\)
=>y=9x-27+1=9x-26
Gọi A(x,y) và B(x,y) lần lượt là tọa độ giao điểm của đường thẳng y=9x-26 với trục Ox và trục Oy
Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\9x-26=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{26}{9}\\y=0\end{matrix}\right.\)
Tọa độ B là; \(\left\{{}\begin{matrix}x=0\\y=9\cdot0-26=-26\end{matrix}\right.\)
Vậy: A(26/9;0); B(0;-26)
\(OA=\sqrt{\left(\dfrac{26}{9}-0\right)^2+\left(0-0\right)^2}=\dfrac{26}{9}\)
\(OB=\sqrt{\left(0-0\right)^2+\left(-26-0\right)^2}=26\)
Vì Ox\(\perp\)Oy nên OA\(\perp\)OB
=>ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot26\cdot\dfrac{26}{9}=\dfrac{338}{9}\)
=>Chọn D