Quan sát hình trên và chứng minh $x = \dfrac {ah }{a' − a}$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
Vì \(\left\{ \begin{array}{l}BC \bot AB'\\B'C' \bot AB'\end{array} \right. \Rightarrow BC//B'C'\)(quan hệ từ vuông góc đến song song).
- Xét tam giác \(AB'C'\) có \(BC//B'C'\) và \(BC\) cắt \(AB';AC'\) lần lượt tại \(B;C\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AB'}} = \frac{{BC}}{{B'C'}} \Rightarrow \frac{x}{{x + h}} = \frac{a}{{a'}} \Rightarrow xa' = a\left( {x + h} \right) \Leftrightarrow xa' = ax + ah\)
\( \Leftrightarrow xa' - ax = ah \Leftrightarrow x\left( {a' - a} \right) = ah \Leftrightarrow x = \frac{{ah}}{{a' - a}}\) (điều phải chứng minh).
AT
6 tháng 7 2021
a) Ta có: \(\angle HEA=\angle HFA=\angle EAF=90\Rightarrow AEHF\) là hình chữ nhật
\(\Delta AHB\) vuông tại H có HE là đường cao \(\Rightarrow AE.AB=AH^2\)
\(\Delta AHC\) vuông tại H có HF là đường cao \(\Rightarrow AF.AC=AH^2\)
\(\Rightarrow AE.AB=AF.AC\)
b) \(\Delta ABC\) vuông tại A có đường cao AH \(\Rightarrow\left\{{}\begin{matrix}AB^2=BH.BC\\AC^2=CH.BC\end{matrix}\right.\)
\(\Rightarrow AB^2-AC^2=BH.BC-CH.BC=BC\left(BH-CH\right)\)
\(=\left(BH+CH\right)\left(BH-CH\right)=BH^2-CH^2\)
c) Ta có: \(\dfrac{1}{HF^2}-\dfrac{1}{CH^2}=\dfrac{1}{AF.FC}-\dfrac{1}{CA.CF}=\dfrac{1}{CF}\left(\dfrac{1}{AF}-\dfrac{1}{CA}\right)\)
\(=\dfrac{1}{CF}.\dfrac{CF}{AF.AC}=\dfrac{1}{AH^2}\)
Lại có: \(\dfrac{1}{HE^2}-\dfrac{1}{BH^2}=\dfrac{1}{BE.EA}-\dfrac{1}{BE.BA}=\dfrac{1}{BE}\left(\dfrac{1}{EA}-\dfrac{1}{BA}\right)\)
\(=\dfrac{1}{BE}.\dfrac{BE}{EA.BA}=\dfrac{1}{AH^2}\)
\(\Rightarrow\dfrac{1}{HF^2}-\dfrac{1}{CH^2}=\dfrac{1}{HE^2}-\dfrac{1}{BH^2}\Rightarrow\dfrac{1}{BH^2}-\dfrac{1}{CH^2}=\dfrac{1}{HE^2}-\dfrac{1}{HF^2}\)
d) Ta có: \(AH^4=\left(AH^2\right)^2=\left(BH.CH\right)^2=BH^2.CH^2\)
\(=BE.BA.CF.CA=BE.CF.\left(AB.AC\right)=BE.CF.AH.BC\)
\(\Rightarrow BC.BE.CF=AH^3\)
e) Ta có: \(AE.BE+AF.CF=EH^2+HF^2=EF^2=AH^2=BH.CH\)
f) Ta có: \(3AH^2+BE^2+CF^2=3AH^2+BH^2-EH^2+CH^2-HF^2\)
\(=3AH^2+BH^2+CH^2-\left(EH^2+HF^2\right)\)
\(=3AH^2+BH^2+CH^2-EF^2=3AH^2+BH^2+CH^2-AH^2\)
\(=BH^2+CH^2+2AH^2=BH^2+CH^2+2BH.CH\)
\(=\left(BH+CH\right)^2=BC^2\)
2 tháng 9 2021
b: Xét ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
hay \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN và ΔACB có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
\(\widehat{MAN}\) chung
Do đó: ΔAMN\(\sim\)ΔACB
AH
Akai Haruma
Giáo viên
11 tháng 9 2021
Lời giải:
Áp dụng hệ thức lượng trong tam giác vuông đối với tam giác vuông $AHB$, đường cao $HE$:
$EA.EB=HE^2$
Tương tự: $FA.FC=HF^2$
$\Rightarrow EA.EB+FA.FC=HE^2+HF^2=EF^2(1)$ (định lý Pitago)
Mặt khác: Dễ thấy $HEAF$ là hình chữ nhật do có 3 góc $\widehat{E}=\widehat{A}=\widehat{F}=90^0$
$\Rightarrow EF=HA$
$\Rightarrow EF^2=HA^2(2)$
Áp dụng hệ thức lượng trong tam giác vuông $ABC$:
$AH^2=HB.HC(3)$
Từ $(1);(2); (3)\Rightarrow EA.EB+FA.FC=HB.HC$ (đpcm)
H9
HT.Phong (9A5)
CTVHS
18 tháng 8 2023
Vì: \(AB=\dfrac{\lambda}{4}\)
Độ lệch pha của hai điểm là:
\(\Delta\varphi=\dfrac{2\pi}{\lambda}AB=\dfrac{2\pi}{\lambda}\cdot\dfrac{\lambda}{4}=\dfrac{2\pi}{4}=\dfrac{\pi}{2}\) rad
19 tháng 9 2023
+) TH1:
M nằm giữa H và N:
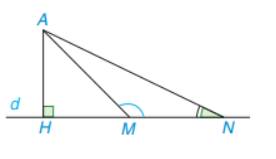
Vì góc AMN là góc ngoài tại đỉnh M của tam giác AHM nên hay là góc tù.
Xét tam giác AMN có là góc tù nên là góc lớn nhất trong tam giác. Cạnh AN đối diện với nên là cạnh lớn nhất trong tam giác ( định lí)
Vậy AM < AN
+) TH2:
H nằm giữa M và N:
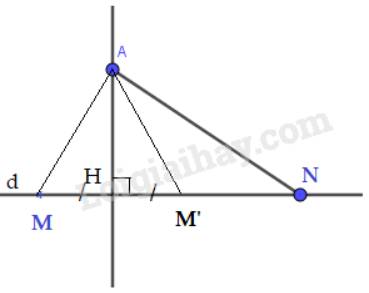
Lấy điểm M’ trên d sao cho HM’ = HM. Ta được AH là đường trung trực của đoạn thẳng MM’ nên AM = AM’ ( tính chất đường trung trực của đoạn thẳng)
Hơn nữa, AM’ < AN ( theo trường hợp 1)
AM < AN
Vậy AM < AN.
b)
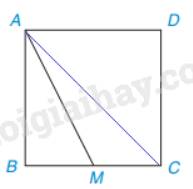
Theo câu a, khi M thay đổi trên BC, M càng xa B thì AM càng lớn. Khi M trùng C thì M xa B nhất nên khi đó AM là lớn nhất.
14 tháng 10 2021
a: Ta có: \(\dfrac{AB}{AC}=\dfrac{5}{6}\)
\(\Leftrightarrow\dfrac{HB}{HC}=\dfrac{25}{36}\)
\(\Leftrightarrow HB=\dfrac{25}{36}HC\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{25}{36}=100\)
\(\Leftrightarrow HC^2=144\)
\(\Leftrightarrow HC=12\left(cm\right)\)
\(\Leftrightarrow HB=\dfrac{10^2}{12}=\dfrac{25}{3}\left(cm\right)\)
CM
27 tháng 1 2019
a) Ta có: OA = OB (= bán kính đường tròn (O))
O’A = O’B (= bán kính đường tròn (O’))
⇒ OO’ là đường trung trực của AB
b) Hình 86a) Hai đường tròn tiếp xúc ngoài thì A nằm giữa O và O’
Hình 86b) Hai đường tròn tiếp xúc trong thì A nằm ngoài đoạn OO’
Ta có
\(BC\perp AB';B'C'\perp AB'\) => BC//B'C'
\(\Rightarrow\dfrac{AB}{AB'}=\dfrac{BC}{B'C'}\Rightarrow\dfrac{x}{x+h}=\dfrac{a}{a'}\)
\(\Rightarrow a'x=ax+ah\Rightarrow x\left(a'-a\right)=ah\Rightarrow x=\dfrac{ah}{a'-a}\left(dpcm\right)\)
Xét tam giác ABCABC có BC⊥ AB′BC⊥ AB′ và B′C′⊥AB′B′C′⊥AB′ nên suy ra BCBC // B′C′B′C′.
Theo hệ quả định lí Thalès, ta có: ABAB′ =BCBC′AB′AB =BC′BC
Suy ra xx+h =aa′x+hx =a′a
a′.x=a(x+h)a′.x=a(x+h)
a′.x−ax=aha′.x−ax=ah
x(a′−a)=ahx(a′−a)=ah
x=aha′ −ax=a′ −aah.