để đo chiều cao AB của một tòa nhà người ta đặt một dụng cụ đo đạc NM thẳng đứng trên mặt đất và xác định được điểm C trên mặt đất sao cho ba điểm A,N,C thẳng hàng và ba điểm B,M,C thẳng hàng. Biết rằng NM=1,5 m, CN=1,25m,CA=20 m
Tính chiều cao AB của tòa nhà đó
Mình đang cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 6 2021
Ta có :
\(\dfrac{NM}{AB}\) và \(\dfrac{CN}{CA}\) .
Vì \(\dfrac{NM}{AB}\) = \(\dfrac{CN}{CA}\) \(\Leftrightarrow\) AB = 1,5 . \(\dfrac{20}{1,25}\) = 24 ( m ) .
Vậy chiều cao AB của tòa nhà đó là 24 m .
1 tháng 2
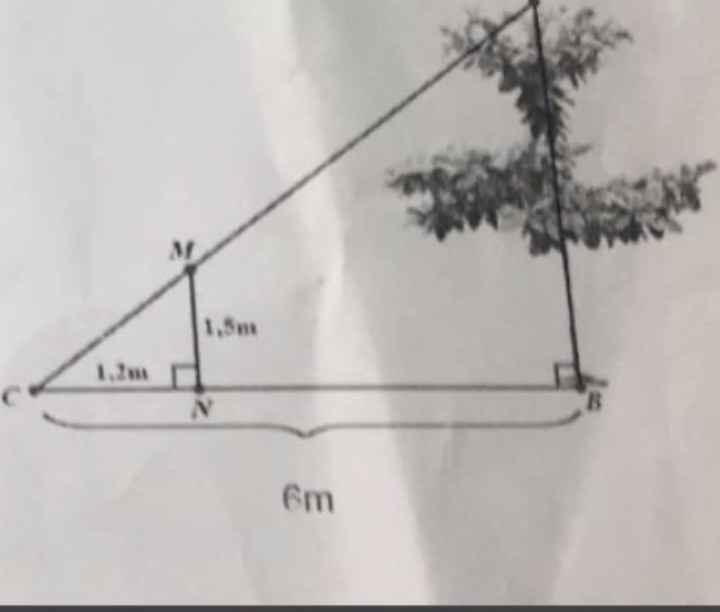
Ta có:MN\(\perp\)CB
AB\(\perp\)CB
Do đó: MN//AB
Xét ΔCAB có MN//AB
nên \(\dfrac{MN}{AB}=\dfrac{CN}{CB}\)
=>\(\dfrac{1.5}{AB}=\dfrac{1.2}{6}=\dfrac{1}{5}\)
=>AB=1,5*5=7,5(m)
22 tháng 6 2023
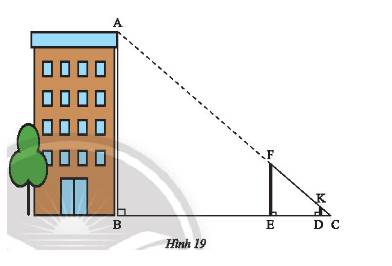
Xét ΔCAB có FE//AB
nên FE/AB=CF/CA
=>6/AB=4/10=2/5
=>AB=15(m)
15 tháng 6 2023
góc ADB=180-73-48=59 độ
AB/sin59=DA/sin48=DB/sin73
=>DA=26,0(m); DB=33,47(m)
S ABC=1/2*26*33,47*sin59=372,96m2
=>AH=2*372,96:30=24,864(m)
CM
18 tháng 10 2017
Ta có: A1B1 = AB = 12 m
Xét ΔDC1A1 có: C1A1 = C1D.cot49o
Xét ΔDC1B1 có: C1B1 = C1D.cot35o
Mà A1B1 = C1B1 - C1A1 = C1D.cot35o - C1D.cot49o
= C1D.(cot35o - cot49o)
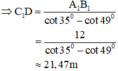
⇒ CD = CC1 + C1D = 1,3 + 21,47 = 22,77 m.
Vậy chiều cao của tháp là 22,77m.
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Ta có: \(\widehat {D{A_1}{C_1}} = \widehat {{A_1}D{B_1}} + \widehat {D{B_1}{A_1}} \Rightarrow \widehat {{A_1}D{B_1}} = {49^ \circ } - {35^ \circ } = {14^ \circ }\)
Áp dụng định lí sin trong tam giác \({A_1}D{B_1}\) , ta có:
\(\begin{array}{l}\frac{{{A_1}D}}{{\sin {B_1}}} = \frac{{{A_1}{B_1}}}{{\sin D}} \Leftrightarrow \frac{{{A_1}D}}{{\sin {{35}^ \circ }}} = \frac{{12}}{{\sin {{14}^ \circ }}}\\ \Rightarrow {A_1}D = \sin {35^ \circ }.\frac{{12}}{{\sin {{14}^ \circ }}} \approx 28,45\end{array}\)
Áp dụng định lí sin trong tam giác \({A_1}D{C_1}\) , ta có:
\(\begin{array}{l}\frac{{{A_1}D}}{{\sin {C_1}}} = \frac{{{C_1}D}}{{\sin {A_1}}} \Leftrightarrow \frac{{28,45}}{{\sin {{90}^ \circ }}} = \frac{{{C_1}D}}{{\sin {{49}^ \circ }}}\\ \Rightarrow {C_1}D = \sin {49^ \circ }.\frac{{28,45}}{{\sin {{90}^ \circ }}} \approx 21,47\end{array}\)
Do đó, chiều cao CD của tháp là: \(21,47 + 1,2 = 22,67\;(m)\)
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
Vì \(\left\{ \begin{array}{l}KD \bot BC\\AB \bot BC\end{array} \right. \Rightarrow KD//AB\).
Xét tam giác \(CAB\) có \(KD//AB \Rightarrow \frac{{KD}}{{AB}} = \frac{{DC}}{{BC}}\) (hệ quả của định lí Thales).
\( \Rightarrow \frac{1}{{AB}} = \frac{{1,2}}{{24}} \Rightarrow AB = \frac{{24.1}}{{1,2}} = 20m\)
Vậy chiều cao \(AB\) của tòa nhà là 20m.
Ta có: NM//AB
=> \(\dfrac{NM}{AB}=\dfrac{CN}{AC}< =>AB=1,5\cdot\dfrac{20}{1,25}=24\left(m\right)\)
Vậy tòa nhà đó cao 24m
xen kiu bạn nha