Bài 2: Cho tam giác ABC vuông tại A, AB= 9cm, AC=12cm, đường trung tuyến AM. Qua M vẽ ME vuông góc với AB tại E, vẽ MF vuông góc với AC tại F a) C/m tứ giác AEMF là hình chữ nhật b) tinh độ dài BC, A...

TK

Tsukishima Kei

18 tháng 12 2023 - olm

Bài 2: Cho tam giác ABC vuông tại A, AB= 9cm, AC=12cm, đường trung tuyến AM. Qua M vẽ ME vuông góc với AB tại E, vẽ MF vuông góc với AC tại F a) C/m tứ giác AEMF là hình chữ nhật b) tinh độ dài BC, AM c) trên tia đối của tia MA lấy điểm H sao cho MA= MH. C/m ABHC là hình chữ nhật d) gọi điểm D là điểm đối xứng của M qua F. C/m ADCM là hình vuông e) tìm thêm điều kiện của tam giác ABC để tứ giác ADCM là hình...

Đọc tiếp

#Toán lớp 8

0

PT

Phạm Thành Hưng

14 tháng 7 2021

Cho tam giác ABC vuông tại A (AB< AC) có trung tuyến AM .Vẽ ME vuông góc với AB tại E, vẽ MF vuông góc với AC tại F.a / Chứng minh rằng: Tứ giác AEMF là hình chữ nhật?b / Gọi N là điểm đối xứng của M qua F. Chứng minh tứ giác ABMN là hình bình hành ? c/ Vẽ AH vuông góc với BC tại H. Chứng minh rằng: Tứ giác HMFE là hình thang cân? d/ Gọi I là trung điểm của NC. Chứng minh I, F, E thẳng...

Đọc tiếp

#Toán lớp 7

2

NL

Nguyễn Lê Phước Thịnh

14 tháng 7 2021

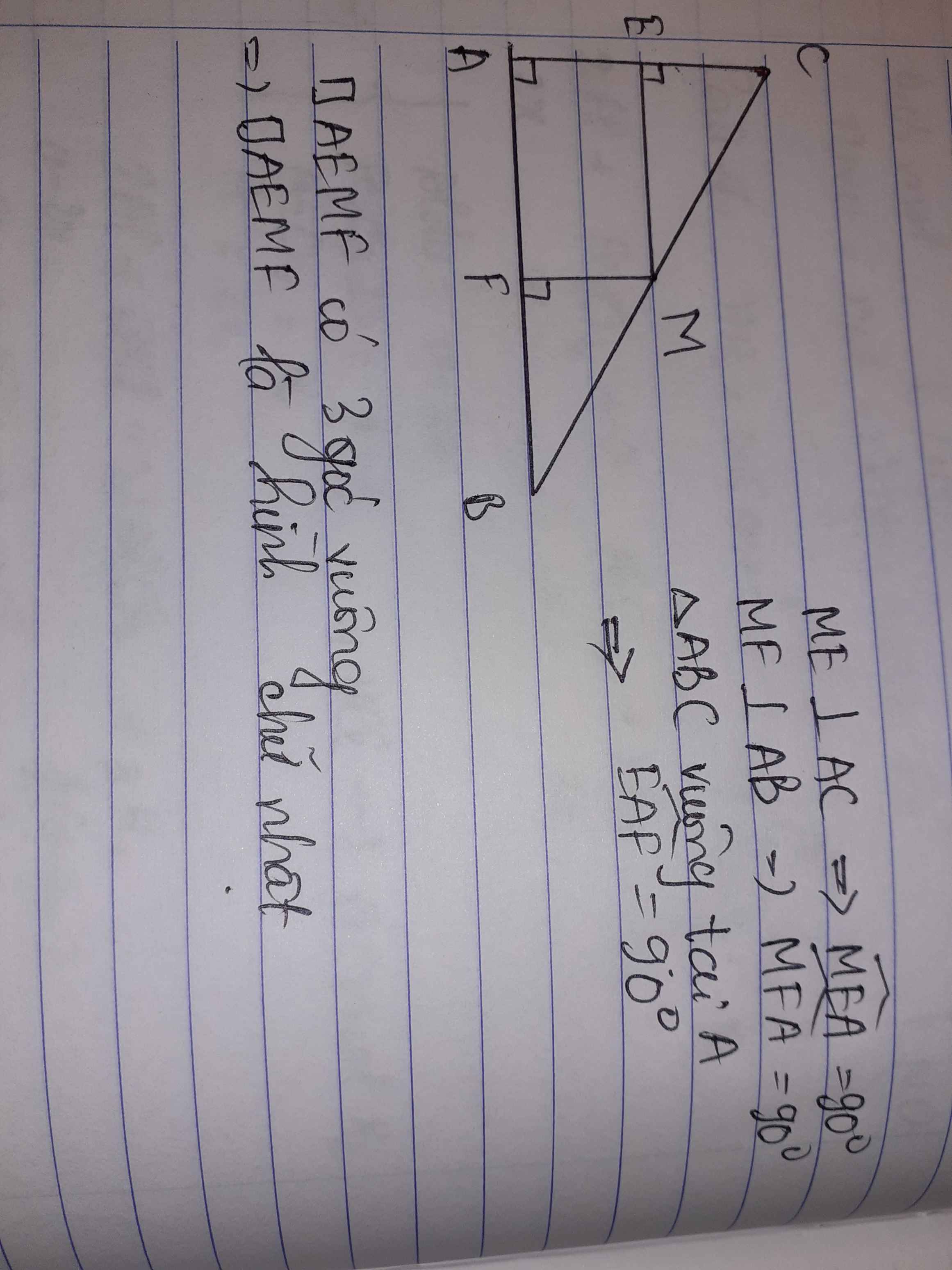
a) Xét tứ giác AEMF có

\(\widehat{EAF}=90^0\)(gt)

\(\widehat{AEM}=90^0\)(gt)

\(\widehat{AFM}=90^0\)(gt)

Do đó: AEMF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

Đúng(0)

NL

Nguyễn Lê Phước Thịnh

14 tháng 7 2021

b) Xét ΔABC có

M là trung điểm của BC(gt)

MF//AB(cùng vuông góc với AC)

Do đó: F là trung điểm của AC(Định lí 1 về đường trung bình của tam giác)

Xét ΔABC có

M là trung điểm của BC(gt)

F là trung điểm của AC(cmt)

Do đó: MF là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)

Suy ra: \(MF=\dfrac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)

mà AE=MF(AFME là hình chữ nhật)

nên \(AE=\dfrac{AB}{2}\)

mà A,E,B thẳng hàng(gt)

nên E là trung điểm của AB

Ta có: F là trung điểm của NM(gt)

nên \(MN=2\cdot MF\)(1)

Ta có: E là trung điểm của AB(cmt)

nên AB=2AE(2)

Ta có: AEMF là hình chữ nhật(cmt)

nên MF=AE(Hai cạnh đối)(3)

Từ (1), (2) và (3) suy ra MN=AB

Xét tứ giác ABMN có

MN//AB(cùng vuông góc với AC)

MN=AB(cmt)

Do đó: ABMN là hình bình hành(Dấu hiệu nhận biết hình bình hành)

Đúng(1)

NT

Nguyễn Thanh Thảo

15 tháng 9 2016 - olm

Cho tam giác ABC vuông tại A có đường trung tuyến AM, từ M kẻ ME vuông góc với AB tại E, MF vuông góc với AC tại F. BIết AB = 9cm, AC = 12cm.

a) Tính AM

b) Chứng minh tứ giác AEMF là hình chữ nhật.

c) Tính EF.

Bạn nào biết làm thì giúp Thảo nhé, Thảo cảm ơn nhìu!

#Toán lớp 8

1

M

MARKTUAN

15 tháng 9 2016

hình bạn tự vẽ nhan

câu a:xét tam giác ABC vuông tại A có BC^2=AB^2+AC^2=>BC^2=15^2=>BC=15

mà AM là trung tuyến hạ từ A của tam giác ABC nên AM=BC/2=15/2

câu b:ta có góc BAC=90 độ (giả thuyết);góc MEA=90 độ(gt);góc MFA=90độ(gt)

nên AEMF là hình chữ nhật

câu c:vì AEMF là hình chữ nhật (câu b)nên AM=EF nên EF=15/2

k minh nhan

Đúng(0)

XN

Xuân Nghi

29 tháng 10 2017 - olm

Cho tam giác ABC vuông tại A có đường trung tuyến AM, từ M kẻ ME vuông góc với AB tại E, MF vuông góc với AC tại F. BIết AB = 9cm, AC = 12cm.

a) Tính AM

b) Chứng minh tứ giác AEMF là hình chữ nhật.

c) từ B kẻ đường thẳng song song với AM , cắt đường FM tại D. Chứng minh D đối xứng với A qua trung điểm H của BM

d) EC cắt AM cà MF theo thứ tự I và K. Chứng minh IC = 4 IK

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

3 tháng 8 2022

a: BC=15cm

=>AM=7,5cm

b: Xét tứ giác AEMF có góc AEM=góc AFM=góc FAE=90 độ

nên AEMF là hình chữ nhật

Đúng(0)

LQ

Lê Quang Dương 8a1

22 tháng 8 2023 - olm

cho tam giác abc vuông tại a (ab < ac).Gọi M là trung điểm của BC. Vẽ MF vuông góc AB tại F, ME vuông góc với AC tại E.Lấy N đối xứng với M qua F.a)cm tứ giác AMBN là hình thoi. b) gọi I là giao điểm hai đường chéo của hình chữ nhật AEMF. Đường thẳng BI cắt EM tại K, H là hình chiếu của K qua NB. CM tam giác AMH cân

#Toán lớp 8

0

PT

phuong thao Nguyen

20 tháng 12 2020

Cho tam giác ABC vuông tại A có AB=5cm, AC=12cm; gọi M là trung điểm của BC. Từ M kẻ ME vuông góc với AB, MF vuông góc với AC(E thuộc AB, F thuộc AC)

a) Tứ giác AEMF là hình gì?

b) tính độ dài đoạn thẳng EF

c) tính diện tích của tứ giác AEMF

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

20 tháng 12 2020

a) Xét tứ giác AEMF có

\(\widehat{EAF}=90^0\)(\(\widehat{BAC}=90^0\), E∈AB, F∈AC)

\(\widehat{AEM}=90^0\)(ME⊥AB)

\(\widehat{AFM}=90^0\)(MF⊥AC)

Do đó: AEMF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=5^2+12^2=169\)

\(\Leftrightarrow BC=\sqrt{169}=13cm\)

Ta có: ΔABC vuông tại A(gt)

mà AM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)

nên \(AM=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)

hay \(AM=\dfrac{13}{2}=6.5cm\)

Ta có: AEMF là hình chữ nhật(cmt)

nên AM=EF(Hai đường chéo của hình chữ nhật AEMF)

mà AM=6,5cm

nên EF=6,5cm

Vậy: EF=6,5cm

c) Xét ΔABC có

M là trung điểm của BC(gt)

ME//AC(ME//AF, C∈AF)

Do đó: E là trung điểm của AB(Định lí 1 đường trung bình của tam giác)

⇒\(AE=\dfrac{AB}{2}=\dfrac{5}{2}=2.5cm\)

Xét ΔABC có

M là trung điểm của BC(gt)

MF//AB(MF//AE, B∈AE)

Do đó: F là trung điểm của AC(Định lí 1 đường trung bình của tam giác)

⇒\(AF=\dfrac{AC}{2}=\dfrac{12}{2}=6cm\)

Ta có: AEMF là hình chữ nhật(cmt)

nên \(S_{AEMF}=AE\cdot AF=2.5\cdot6=15cm^2\)

Đúng(2)

NK

Nguyễn Ka

29 tháng 12 2022 - olm

Bài 3 Cho tam giác ABC vuông tại A,M là trung điểm của BC. Qua M kẻ ME vuông góc với AB tại E, kẻ MF vuông góc với AC tại F.

a) Tứ giác AEMF là hình gì? Vì sao?

b) Đường thẳng qua A song song với BC cắt đường thảng qua C song song AB tại N. Chứng minh rằng M, F, N thẳng hàng

#Toán lớp 8

0

NL

Nguyễn Lan

19 tháng 11 2021

Cho tam giác ABC vuông tại A. Từ điểm M trên BC, vẽ ME huống góc với AC tại E và MF huống góc với AB tại F. a)chứng minh tứ giác AEMF là hình chữ nhật. b) Gọi I là trung điểm của EF. Chứng tỏ 3 điểm A,I,M thẳng hàng. c) kẻ IH vuông góc AC tại H. Gọi K là điểm đối xứng với I qua H. Chứng minh tứ giác AIEK là hình thoi.

#Toán lớp 8

0

PT

Phương Thảo

19 tháng 11 2016

Cho tam giác ABC vuông tại A . Gọi M là trung điểm BC . Qua M kẻ ME vuông góc AB ( E ϵ AB ) , MF vuông góc AC ( F ϵ AC ).
a. Chứng minh tứ giác AEMF là hình chữ nhật .
b. Gọi N là điểm đối xứng của M qua F . Tứ giá MANC là hình gì ? Tại sao ?
c. Tìm điều kiện của tam giác ABC để tứ giác AEMF là hình vuông.

#Toán lớp 8

2

NT

nguyễn thị hoàng hà

19 tháng 11 2016

(Hình bạn tự vẽ nha)

a ,

Tứ giác AEMF có góc A = góc AME = góc AFM = 90 độ nên là hình chữ nhật .

b ,

Xét tam giác vuông ABC có đường trung tuyến AM ứng với cạnh huyền BC nên AM = MC = MB

Vì N là điểm đối xứng của M qua F nên MN vuông góc với AC và MF=NF .

-> AC là đường trung trực của MN

->MC = NC , AM = AN (áp dụng tính chất của đường trung trực ) mà AM = MC nên MC=NC=AM=AN .

-> Tứ giác MANC là hình thoi.

c ,

Để hình chữ nhật AEMF là hình vuông thì AE = AF (1)

Vì AM=BM và ME vuông góc với AB nên ME là đường trung trực của AB .

-> AE = EB (2)

Vì tứ giác MANC là hình thoi nên AF=FC (3)

Từ (1),(2) và (3) suy ra BE = FC (4)

Từ (1) và (4) suy ra : AE + BE = AF + FC

hay AB = AC

-> Tam giác ABC là tam giác vuông cân .

Vậy để tứ giác AEMF là hình vuông thì tam giác ABC là tam giác vuông cân .

Đúng(0)

NT

Nguyễn Thị Thu Hiền

19 tháng 11 2016

Hỏi đáp Toán

Đúng(1)

PT

Phạm Thành Hưng

13 tháng 7 2021

Cho tam giác abc vuông tại a có m là trung điểm của bc (ab>ac).vẽ me vuông góc với ac tại e,mf vuông góc với ad tại f . Cm tứ giác afme là hình chữ nhật

#Toán lớp 7

2