giúp tui đi pls :((
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KC
1
VN
Võ Ngọc Phương
VIP
27 tháng 4 2023
Vì ruột phích có tráng một lớp thuỷ ngân mỏng, nên bức xạ của nhiệt lượng bị lớp thuỷ ngân phản xạ mà chịu nằm lại trong ruột phích.
⇒ Làm cho con đường của bức xạ nhiệt cũng bị ngăn chặn triệt để.
Chúc bạn học tốt
MD
1
15 tháng 10 2023
\(\dfrac{2+\sqrt{2}}{\sqrt{2}+1}+\dfrac{1}{\sqrt{3}+\sqrt{2}}\)
\(=\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}+\dfrac{\sqrt{3}-\sqrt{2}}{3-2}\)
\(=\sqrt{2}+\sqrt{3}-\sqrt{2}=\sqrt{3}\)
TD
3
12 tháng 12 2021
Ta có : B(4) : 0;4;8;12;16;...; -4;-8;-12;-16;...
Ư(-36) : -1;-2;-3;-4;-6;-9;-12;-18;-36; 1;2;3;4;6;9;12;18;36
x = -4; -12;-36; 4;12;16
~ HT~
DH
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
6 tháng 12 2023
a/
\(A=\left(4+4^2\right)+4^2\left(4+4^2\right)+...+4^{22}\left(4+4^2\right)=\)
\(=20\left(1+4^2+4^4+...+4^{22}\right)⋮20\)
b/
\(A=\left(4+4^2+4^3\right)+...+\left(4^{22}+4^{23}+4^{24}\right)=\)
\(=4\left(1+4+4^2\right)+...+4^{22}\left(1+4+4^2\right)=\)
\(=21\left(4+4^4+...+4^{22}\right)⋮21\)
c/
A đồng thời chia hết cho 20 và 21, mà 20 và 21 là 2 số nguyên tố cùng nhau
\(\Rightarrow A⋮20.21=420\)
8 tháng 12 2018
Bài làm
a) Xét tam giác BAD và tam giác CAD
Ta có: AB = AC ( giả thiết )
\(\widehat{A_1}=\widehat{A_2}\) ( Vì AD là tia phân giác của \(\widehat{BAC}\) )
AD là cạnh chung
= > Tam giác BAD = tam giác CAD ( c.g.c )
Vậy tam giác BAD = tam giác CAD
b) Vì tam giác BAD = tam giác CAD ( theo câu a) )
=> \(\widehat{ADB}=\widehat{ADC}\)( hai góc tương ứng )
Vậy \(\widehat{ADB}=\widehat{ADC}\)
c) Ta có: \(\widehat{ADB}+\widehat{ADC}=180^0\)( hai góc kề bù )
Mà \(\widehat{ADB}=\widehat{ADC}\)( theo câu b) )
=> \(\widehat{ADB}=\widehat{ADC}=\frac{180^0}{2}=90^0\)
=> AD vuông góc với BC
Vậy AD vuông góc với BC
# Chúc bạn học tốt #
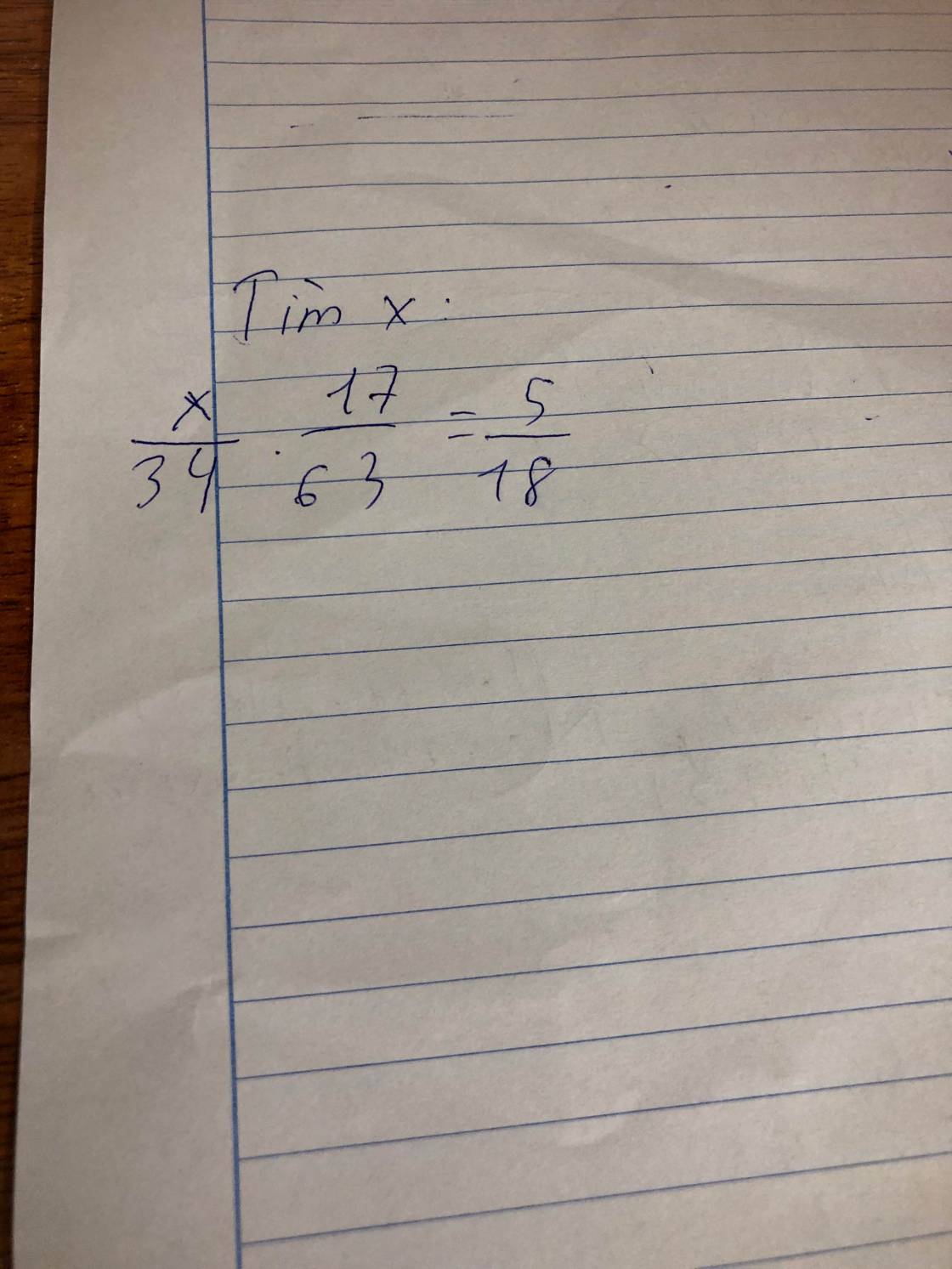
a: \(M=2\left(x+5\right)^2+5\left(x-2\right)^2-7\left(x+3\right)\left(x-3\right)\)
\(=2\left(x^2+10x+25\right)+5\left(x^2-4x+4\right)-7\left(x^2-9\right)\)
\(=2x^2+20x+50+5x^2-20x+20-7x^2+63\)
\(=113\)
b: \(H=\left(2x-3y\right)^2-\left(3y-2\right)\left(3y+2\right)-\left(1-2x\right)^2+4x\left(3y-1\right)\)
\(=4x^2-12xy+9y^2+12xy-4x-\left(9y^2-4\right)-\left(4x^2-4x+1\right)\)
\(=4x^2+9y^2-4x-9y^2+4-4x^2+4x-1\)
=3
c: \(N=\left(2x+3y\right)^2+\left(3x-2y\right)^2-13\left(x+y\right)\left(x-y\right)-26\left(y+1\right)\left(y-1\right)\)
\(=4x^2+12xy+9y^2+9x^2-12xy+4y^2-13\left(x^2-y^2\right)-26\left(y^2-1\right)\)
\(=13x^2+13y^2-13x^2+13y^2-26y^2+26\)
=26
d: \(K=\left(x^2y-3\right)^2-\left(2x-y\right)^3+xy^2\left(6-x^3\right)+8x^3-6x^2y-y^3\)
\(=x^4y^2-6x^2y+9+6xy^2-x^4y^2+8x^3-6x^2y-y^3-\left(2x-y\right)^3\)
\(=-12x^2y+9-y^3+6xy^2+8x^3-\left(8x^3-12x^2y+6xy^2-y^3\right)\)
\(=\left(8x^3-12x^2y+6xy^2-y^3\right)-\left(8x^3-12x^2y+6xy^2-y^3\right)+9\)
=9
e: \(P=\left(4x+3\right)\left(16x^2-12x+9\right)-\left(-23+64x^3\right)\)
\(=\left(4x\right)^3+3^3+23-64x^3\)
\(=64x^3+27+23-64x^3\)
=50
h: \(Q=\left(x+5y\right)\left(x^2-5xy+25y^2\right)+\left(x-5y\right)\left(x^2+5xy+25y^2\right)-\dfrac{1}{2}\left(4x^3-7\right)\)
\(=x^3+125y^3+x^3-125y^3-2x^3+\dfrac{7}{2}\)
=7/2
cảm on ạa