cho tứ diện ABCD gọi E là trung điểm DC, M là điểm nằm giữa A và E hình chiếu song song của M lên (BCD) theo phương chiếu AD là M' khẳng định nào sau đây đúng?
A. M' thuộc đoạn BE
B. M' thuộc đoạn BC
C. M' thuộc đoạn BD
D. M' thuộc đoạn CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 11 2023
Gọi K là trung điểm của CD
Xét ΔADC có
Q,K lần lượt là trung điểm của DA,DC
=>QK là đường trung bình của ΔADC
=>QK//AC
=>Hình chiếu song song của điểm Q theo phương AC lên mp(BCD) là điểm K
15 tháng 11 2023
Gọi N là trung điểm của BC
Xét ΔABC có
N,P lần lượt là trung điểm của BC,BA
=>NP là đường trung bình của ΔABC
=>NP//AC
=>Hình chiếu song song của điểm P theo phương AC lên mp(BCD) là điểm N
CM
22 tháng 10 2019
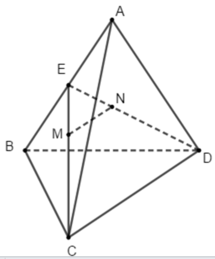
Gọi E là trung điểm của AB.M, N lần lượt là trọng tâm của tam giác ABC, ABD nên:
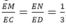
Theo định lí Ta-lét ta có MN // CD. Vậy hình chiếu song song của điểm M theo phương CD lên mặt phẳng (ABD) là trọng tâm của tam giác ABD. Đáp án C.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
25 tháng 10 2023
Ta có
\(E\in MN\) mà \(MN\in\left(OMN\right)\Rightarrow E\in\left(OMN\right)\)
\(O\in\left(OMN\right)\)
\(\Rightarrow EO\in\left(OMN\right)\)
Ta có
\(E\in BD\) mà \(BD\in\left(BCD\right)\Rightarrow E\in\left(BCD\right)\)
\(O\in\left(BCD\right)\)
\(EO\in\left(BCD\right)\)
Trong (BCD) kéo dài EO cắt CD tại K
=> \(K\in\left(OMN\right);K\in CD\) => K chính là giao của CD với (OMN)
A