Bài 1. Bác Nam dự định trồng ớt và cà trên diện tích $8a$ ($1a=100{{m}^{2}}$). Nếu trồng ớt thì cần $20$ công và thu lãi $3$ $000$ $000$ đồng trên mỗi $a$, nếu trồng cà thì cần $30$ công và thu lãi $4$ $000$ $000$ đồng trên mỗi $a$. Biết tổng số công cần dùng không được vượt quá $180$. Tính số tiền lãi lớn nhất thu được.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là diện tích trồng đậu, y là diện tích trồng cà, (đơn vị a = 100 m 2 ), điều kiện x ≥ 0, y ≥ 0, ta có x + y ≤ 0
Số công cần dùng là 20x + 30y ≤ 180 hay 20 + 3y ≤ 18
Số tiền thu được là
F = 3000000x + 4000000y (đồng)
Hay F = 3x + 4y (đồng)
Ta cần tìm x, y thỏa mãn hệ bất phương trình
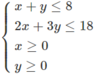
Sao cho F = 3x + 4y đạt giá trị lớn nhất.
Biểu diễn tập nghiệm của (H) ta được miền tứ giác OABC với A(0;6), B(6;2), C(8;0) và O(0;0).
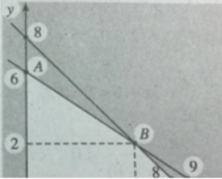
Xét giá trị của F tại các đỉnh O, A, B, C và so sánh ta suy ra x = 6, y = 2 (tọa độ điểm B) là diện tích cần trồng mỗi loại để thu được nhiều tiền nhất là F = 26 (triệu đồng).
Đáp số: Trồng 6a đậu, 2a cà, thu hoạch 26 000 000 đồng.

số cà chua và cây ớt có trong mỗi nhà kính là
\(\left(\dfrac{8592}{4}\right)+\left(\dfrac{19896}{4}\right)=2148+4974=7122\left(cây\right)\)
vì số ớt và số cà chua được trông trong nhà kinha là như nhau nên
số cây cà chua có trong mỗi nhà kính là
\(\dfrac{7122}{2}=3561\)(cây cà chua)
số cây ớt có trong mỗi nhà kính là
\(\dfrac{7122}{2}=3561\)(cây ớt)

Mỗi nhà kính trồng số ớt là:
\(8592:4=2148\left(\text{cây}\right)\)
Mỗi nhà kính trồng số cà chua là:
\(19896:4=4974\left(\text{cây}\right)\)

