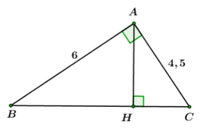
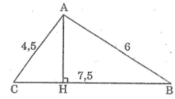
ho tam giác ABC vuông tại A, đ/cao AH có AB=4,5cm;AC=6cm.
a) Tính độ dài các đoạn thẳng BC,AH
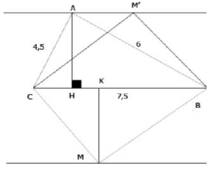
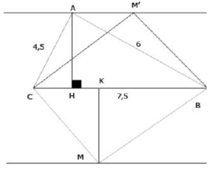
Kẻ HD vuông góc vs AB(D thuộc AB), HE vuông góc vs AC (E thuộc AC). CM DE tiếp xúc vs đ/tròn đi qua 3 điểm E,H,C
c) Gọi I là giao điểm của AH,DE, M là trung điểm của HC.Tính độ dài MI
giúp tui giải bài này vs tui ddag cần gấp ![]()
![]()

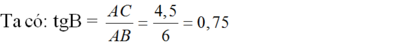
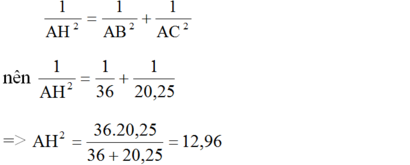
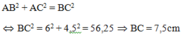
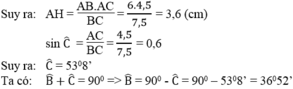
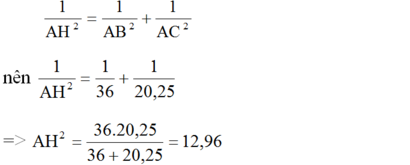
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=4,5^2+6^2=7,5^2\)
=>\(BC=\sqrt{7,5^2}=7,5\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot7,5=4,5\cdot6=27\)
=>\(AH=\dfrac{27}{7,5}=3,6\left(cm\right)\)
b: Gọi M là trung điểm của HC
Vì ΔCEH vuông tại E
nên ΔCEH nội tiếp đường tròn đường kính HC
=>ΔCEH nội tiếp (M)
=>ME=MH=MC
Vì ME=MH
nên \(\widehat{MEH}=\widehat{MHE}\)
mà \(\widehat{MHE}=\widehat{ABC}\)(hai góc đồng vị, HE//AB)
nên \(\widehat{MEH}=\widehat{ABC}\)
Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
=>\(\widehat{DAH}=\widehat{DEH}\)
=>\(\widehat{DEH}=\widehat{HAB}\)
\(\widehat{MED}=\widehat{MEH}+\widehat{DEH}\)
\(=\widehat{HBA}+\widehat{HAB}=90^0\)
=>DE là tiếp tuyến của (M)(ĐPCM)
c: Vì ADHE là hình chữ nhật
nên AH cắt DE tại trung điểm của mỗi đường
=>I là trung điểm chung của AH và DE
Xét ΔHAC có
I,M lần lượt là trung điểm của HA,HC
=>IM là đường trung bình của ΔHAC
=>\(IM=\dfrac{AC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
tui c.ơn nhiều