Cho P(x) = x3+ 3ax + a2
Q(x) = 2x2 - (2a+3) x +a2
tìm a , biết P(1) ; Q(-2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(A\left(1\right)=B\left(-2\right)\Leftrightarrow12+2a+a^2=8-\left|2a+3\right|\left(-2\right)+a^2\)
\(\Leftrightarrow4+2a=2\left|2a+3\right|\)
đk a >= -2
\(\left[{}\begin{matrix}4a+6=4+2a\\4a+6=-2a-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=-1\left(tm\right)\\a=-\dfrac{5}{3}\left(ktm\right)\end{matrix}\right.\)

11: \(2x^2-12xy+18y^2\)
\(=2\left(x^2-6xy+9y^2\right)\)
\(=2\left(x-3y\right)^2\)
12: \(\left(x^2+x\right)^2+3\left(x^2+x\right)+2\)
\(=\left(x^2+x+2\right)\left(x^2+x+1\right)\)

Sửa đề:
Tìm a biết P(1)=Q(-2)
Ta có:
\(P\left(1\right)=1^3+3a.1+a^2=a^2+3a+1\)
\(Q\left(-2\right)=2.\left(-2\right)^2-\left(2a+3\right).\left(-2\right)+a^2\)
\(=2.4+2\left(2a+3\right)+a^2\)
\(=8+4a+6+a^2=a^2+4a+14\)
Mà \(P\left(1\right)=Q\left(-2\right)\)
\(\Rightarrow a^2+3a+1=a^2+4a+14\)
\(\Rightarrow3a-4a=14-1\Rightarrow-a=13\Rightarrow a=-13\)
Vậy................
Chúc bạn học tốt!!!

ta có: P(1) = 13+3a.1+a2
P(1) = 1 + 3a + a2
Lại có: Q(-2) = 2.(-2)2 - (2a+3).(-2) + a2
Q(-2) = 8 +4a + 6 + a2
Q(-2) = 15 + 4a + a2
mà P(1) = Q(-2)
=> 1 + 3a + a2 = 15 + 4a + a2
=> 3a + a2 - 4a - a2 = 15-1
-a = 14
a = -14
KL: a = -14

a) Ta có:
B = (A + B) – A
= (x3 + 3x + 1) – (x4 + x3 – 2x – 2)
= x3 + 3x + 1 – x4 - x3 + 2x + 2
= – x4 + (x3 – x3) + (3x + 2x) + (1 + 2)
= – x4 + 5x + 3.
b) C = A - (A – C)
= x4 + x3 – 2x – 2 – x5
= – x5 + x4 + x3 – 2x – 2.
c) D = (2x2 – 3) . A
= (2x2 – 3) . (x4 + x3 – 2x – 2)
= 2x2 . (x4 + x3 – 2x – 2) + (-3) .(x4 + x3 – 2x – 2)
= 2x2 . x4 + 2x2 . x3 + 2x2 . (-2x) + 2x2 . (-2) + (-3). x4 + (-3) . x3 + (-3). (-2x) + (-3). (-2)
= 2x6 + 2x5 – 4x3 – 4x2 – 3x4 – 3x3 + 6x + 6
= 2x6 + 2x5 – 3x4 + (-4x3 – 3x3) – 4x2+ 6x + 6
= 2x6 + 2x5 – 3x4 – 7x3 – 4x2+ 6x + 6.
d) P = A : (x+1) = (x4 + x3 – 2x – 2) : (x + 1)
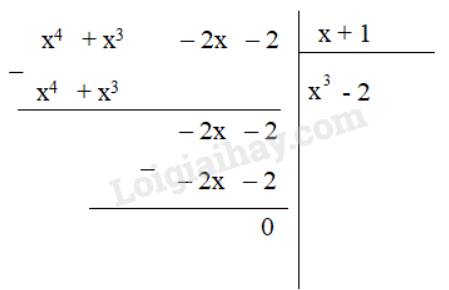
Vậy P = x3 - 2
e) Q = A : (x2 + 1)
Nếu A chia cho đa thức x2 + 1 không dư thì có một đa thức Q thỏa mãn
Ta thực hiện phép chia (x4 + x3 – 2x – 2) : (x2 + 1)
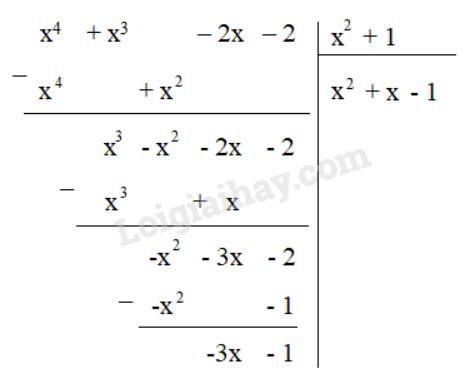
Do phép chia có dư nên không tồn tại đa thức Q thỏa mãn

a) P(x)=4x2-6x+a; Q(x)=x-3
Lấy P(x):Q(x)=4x-6 dư a+30
Vậy để P(x)⋮Q(x) ⇒ a+30=0 ⇒ a=-30
b) P(x)=2x2+x+a; Q(x)=x+3
Lấy P(x):Q(x)=2x-7 dư a+21
Vậy để P(x)⋮Q(x) ⇒ a+21=0 ⇒ a=-21
c) P(x)=x3+ax2-4; Q(x)=x2+4x+4
Lấy P(x):Q(x)=x+a-4 dư -4(a-5)x+12
Vậy để P(x)⋮Q(x) ⇒ -4(a-5)x+12=0 ⇒ (a-5)x=3
⇒ a-5 ϵ {-1;1;-3;3} (a ϵ Z)
⇒ a ϵ {4;6;2;8}
d) P(x)=2x2+ax+1; Q(x)=x-3
Lấy P(x):Q(x)=2x+a+6 dư 3a+19
Vậy để P(x)⋮Q(x) ⇒ 3a+19=0 ⇒ a=-19/3
e) P(x)=ax5+5x4-9; Q(x)=x-1
Lấy P(x):Q(x)=ax4+(a-5)x3+(a-5)x2+(a-5)x+1 dư a-4
Vậy để P(x)⋮Q(x) ⇒ a-4=0 ⇒ a=4
f) P(x)=6x3-x2-23x+a; Q(x)=2x+3
Lấy P(x):Q(x)=3x2-5x-4 dư a+12
Vậy để P(x)⋮Q(x) ⇒ a+12=0 ⇒ a=-12
g) P(x)=x3-6x2+ax-6 Q(x)=x-2
Lấy P(x):Q(x)=x2-2x+a-4 dư 2(a-4)-6
Vậy để P(x)⋮Q(x) ⇒ 2(a-4)-6=0 ⇒ a=7
Bài h có a,b bạn xem lại đề

Áp dụng định lý Bezout ta có:
\(A\left(x\right)⋮\left(x+1\right)\Rightarrow A\left(-1\right)=0\)
\(\Leftrightarrow a^2\left(-1\right)^3+3a\left(-1\right)^2-6.\left(-1\right)-2a=0\)
\(\Leftrightarrow-a+3a+6+2a=0\)
\(\Leftrightarrow4a+6=0\)
\(\Leftrightarrow a=\frac{-3}{2}\)
Vậy \(a=\frac{-3}{2}\)để \(A\left(x\right)⋮\left(x+1\right)\)

a: A=x^3-2x^2+5x-1
B=x^3-3x^2+3x-2
P=A+B=2x^3-5x^2+8x-3
Q=A-B=x^2+2x+1
b: Bậc của P lớn hơn Q
c: Q(-1)=(-1)^2+2*(-1)+1=0
=>x=-1 là nghiệm của Q