 vẽ hình giúp mik nx nha
vẽ hình giúp mik nx nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bạn viết lại đề bằng công thức toán. Chụp hình ntn chữ hơi xấu khó đọc á.

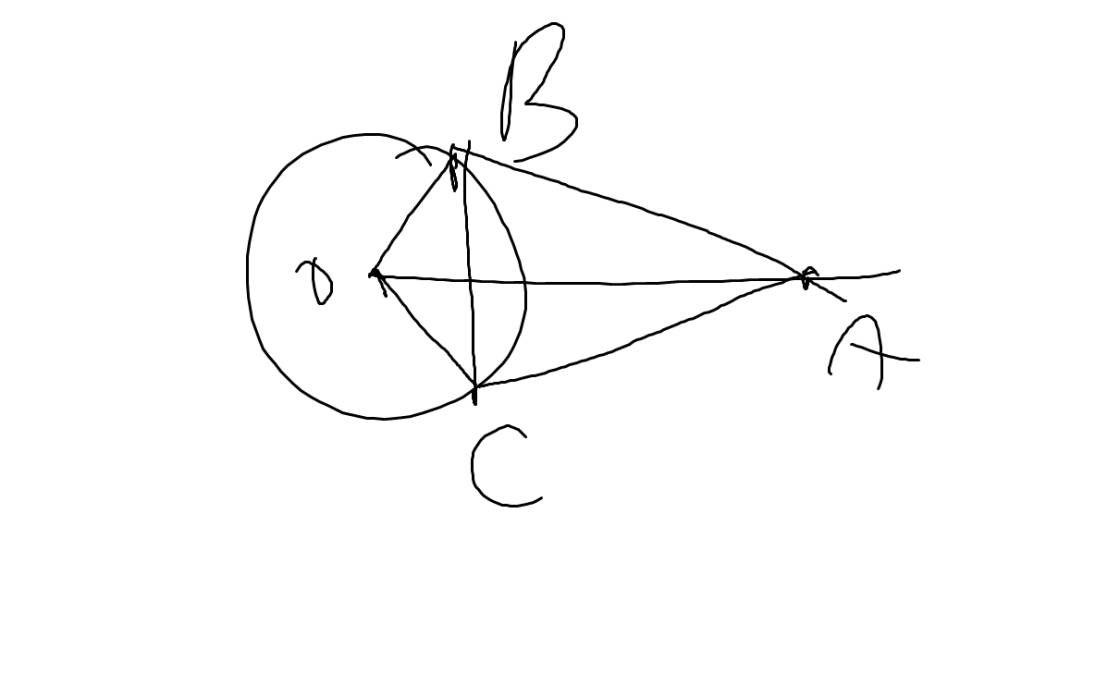
a: AB và AC là hai tiếp tuyến cắt nhau tại A
b: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>OBAC là tứ giác nội tiếp
=>O,B,A,C cùng thuộc 1 đường tròn

Câu 4:
a: Xét ΔMIN và ΔMIP có
MI chung
IN=IP
MN=MP
Do đó: ΔMIN=ΔMIP

a, Xét t/g AMB và t/g AMC có:
AB=AC(gt)
BAM=CAM(gt)
AM chung
=>t/g AMB=t/g AMC (c.g.c)
b, Xét t/g BEM và t/g CMF có:
góc BEM = góc CFM = 90 độ (gt)
MB = MC (t/g AMB=t/g AMC)
góc EBM = góc FCM (gt)
=>t/g BEM = t/g CFM (cạnh huyền - góc nhọn)
=>ME=MF (2 cạnh tương ứng)
c, BI // FC => góc IBM = góc FCM (so le trong)
Xét t/g BIM và t/g CFM có:
góc IBM = góc FCM (vừa chứng minh)
MB = MC (t/g AMB = t/g AMC)
BMI = CMF (đối đỉnh)
=>t/g BIM = t/g CFM (g.c.g)
=>BI = BF (2 cạnh tương ứng)
Mà BE = CF (t/g BEM = t/g CFM)
=> BE = BI
d, Vì MI = MF (t/g BIM = t/g CFM), ME = MF (câu b)
=> MI = ME
Mà \(MI=\frac{IF}{2}\)
=> \(ME=\frac{IF}{2}\)


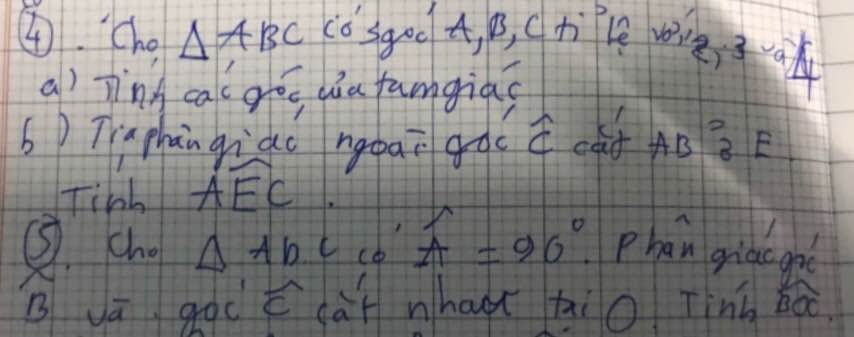

a: Xét tứ giác BCEF có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
=>BCEF là tứ giác nội tiếp
=>B,C,E,F cùng thuộc một đường tròn
b: Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
=>AEHF là tứ giác nội tiếp
=>A,E,H,F cùng thuộc một đường tròn
c: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB đồng dạng với ΔAFC
=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
=>\(AE\cdot AC=AB\cdot AF\)
d: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>AB\(\perp\)BD
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD
Ta có: BE\(\perp\)AC
CD\(\perp\)CA
Do đó: BE//CD
=>BH//CD
Ta có: CH\(\perp\)AB
BD\(\perp\)AB
Do đó: CH//BD
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HD
Xét ΔDAH có
M,O lần lượt là trung điểm của DH,DA
=>MO là đường trung bình của ΔDAH
=>MO=AH/2
=>AH=2MO