Câu1:Cho đường tròn(O;5cm) và dây AB cách tâm Ở một khoảng bằng 3cm.Tính độ dài dây AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 12 2023
Câu 1:
XétΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=4\cdot9=36\)
=>\(AH=\sqrt{36}=6\left(cm\right)\)
Câu 2: Độ dài cạnh hình vuông là:
\(\sqrt{16}=4\left(cm\right)\)
Độ dài đường chéo của hình vuông là:
\(\sqrt{4^2+4^2}=4\sqrt{2}\left(cm\right)\)
Bán kính đường tròn ngoại tiếp hình vuông là:
\(\dfrac{4\sqrt{2}}{2}=2\sqrt{2}\left(cm\right)\)
Câu 5:
Vì \(13^2=12^2+5^2\)
nên đây là tam giác vuông
=>Bán kính đường tròn ngoại tiếp là R=13/2=6,5(cm)
21 tháng 12 2023
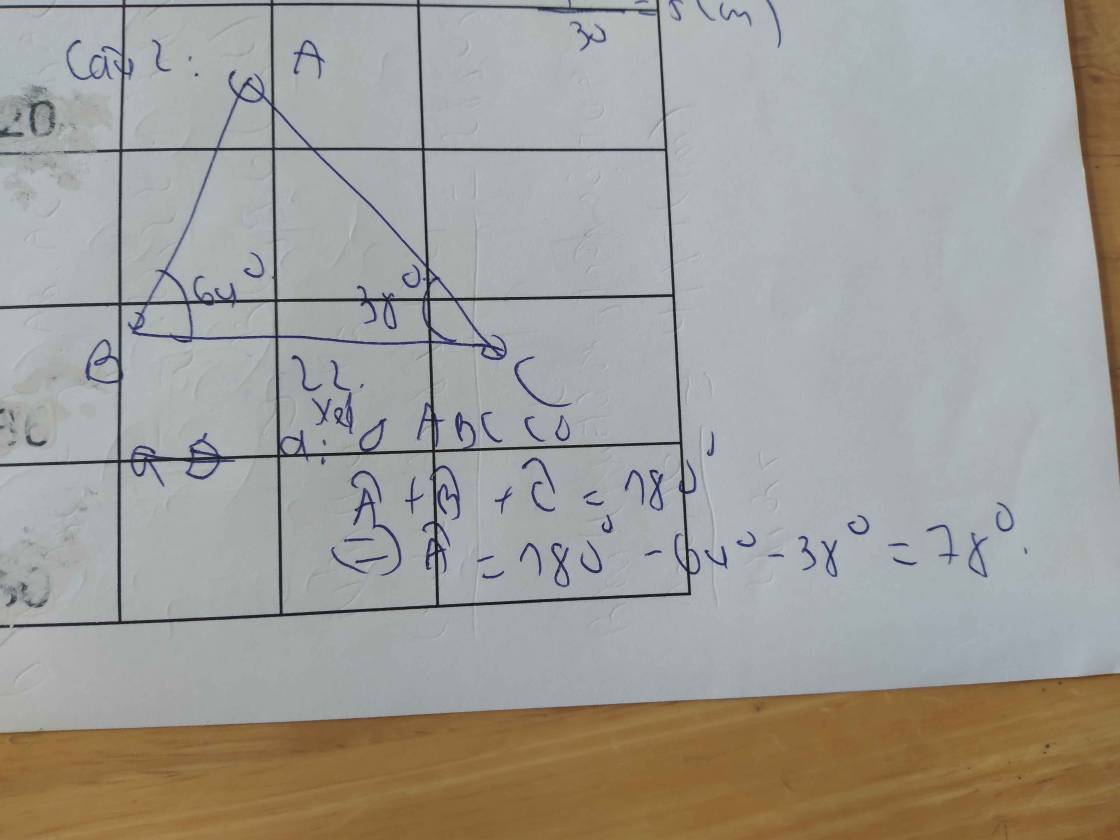
Câu 1:
Xét ΔABC vuông tại A có
\(tanB=\dfrac{AC}{AB}\)
=>\(\dfrac{AC}{6}=\dfrac{4}{3}\)
=>\(AC=\dfrac{4}{3}\cdot6=8\left(cm\right)\)
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Câu 4:
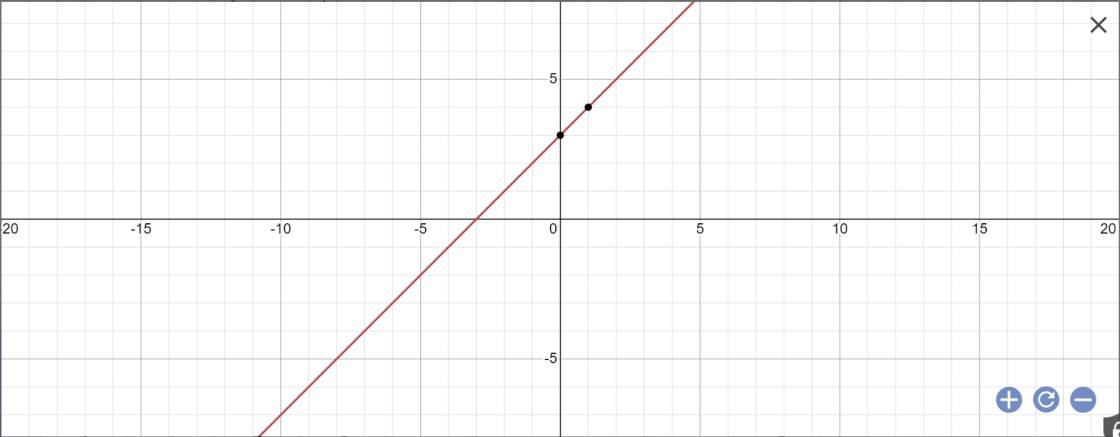
a: Thay x=2 và y=5 vào y=(2m-1)x+3, ta được:
2(2m-1)+3=5
=>2(2m-1)=2
=>2m-1=1
=>2m=2
=>\(m=\dfrac{2}{2}=1\)
b: Khi m=1 thì \(y=\left(2\cdot1-1\right)x+3=x+3\)
15 tháng 12 2023
a: Xét (O) có
CA,CE là các tiếp tuyến
Do đó: CA=CE và OC là phân giác của góc AOE
Xét (O) có
DE,DB là các tiếp tuyến
Do đó: DE=DB và OD là phân giác của góc EOB
Ta có: CA+DB
=CE+DE
=CD
b: Ta có: OC là phân giác của góc AOE
=>\(\widehat{AOE}=2\cdot\widehat{EOC}\)
OD là phân giác của góc EOB
=>\(\widehat{EOB}=2\cdot\widehat{EOD}\)
Ta có: \(\widehat{AOE}+\widehat{BOE}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{EOC}+2\cdot\widehat{EOD}=180^0\)
=>\(2\cdot\left(\widehat{EOC}+\widehat{EOD}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
14 tháng 12 2023
Câu 2:
Thay x=1 và y=1 vào y=ax+2, ta được:
\(a\cdot1+2=1\)
=>a+2=-1
=>a=-1
Vậy: Hệ số góc của đường thẳng d là -1
Câu 1:
Gọi A là tiếp điểm của tiếp tuyến kẻ từ M của (O)
=>MA\(\perp\)OA tại A
Ta có: ΔMAO vuông tại A
=>\(AM^2+AO^2=MO^2\)
=>\(AM^2=10^2-6^2=64\)
=>\(AM=\sqrt{64}=8\left(cm\right)\)
17 tháng 12 2023
Câu 1: Để đường thẳng y=(m2+1)x+m có hệ số góc bằng 1 thì
\(m^2+1=1\)
=>\(m^2=0\)
=>m=0
Câu 2: Thay x=4 và y=0 vào y=x-2m, ta được:
4-2m=0
=>2m=4
=>m=2
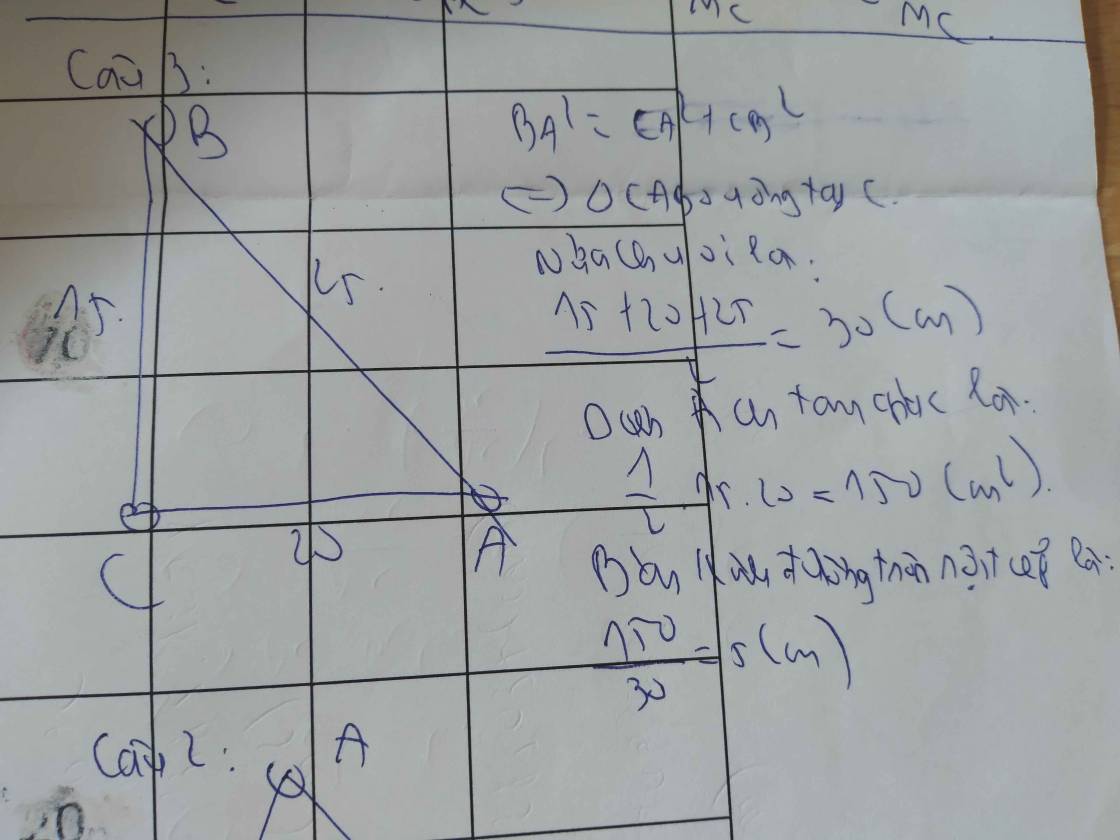
Câu 3:
ΔABC vuông cân tại A
=>AB=AC=10cm và \(BC^2=AB^2+AC^2\)
=>\(BC^2=10^2+10^2=200\)
=>\(BC=10\sqrt{2}\left(cm\right)\)
Ta có: ΔABC vuông cân tại A
=>\(R=\dfrac{BC}{2}=5\sqrt{2}\left(cm\right)\)
Gọi OH là khoảng cách từ O đến AB
=>OH\(\perp\)AB tại H
Theo đề, ta có: OA=OB=5cm và OH=3cm
Ta có: ΔOHA vuông tại H
=>\(HA^2+HO^2=OA^2\)
=>\(HA^2+3^2=5^2\)
=>\(HA^2=25-9=16\)
=>\(HA=\sqrt{16}=4\left(cm\right)\)
Ta có: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
=>\(AB=2\cdot AH=8\left(cm\right)\)