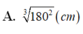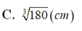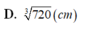Hình 14a mô tả hình dạng của một hộp sữa và lượng sữa chứa trong hộp đó.Hfinh 14b mô tả hình dạng hộp sữa chứa trong hộp khi đặt hộp ngc lại.Tính tỉ số của thể tích có trong hộp và thể tích của cả hộp(Hình ở bài 17 trang 70 sách cánh diều tập 1 nhé mn)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
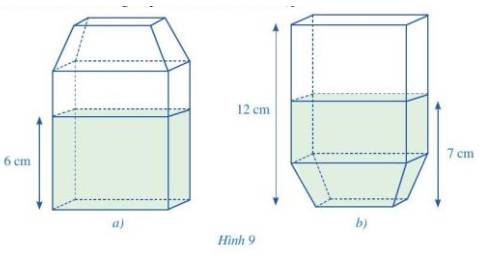
Xét hình 9b, phần hộp không chứa sữa có dạng hình hộp chữ nhật với đáy là đáy của hộp sữa và chiều cao là 12 – 7 = 5 (cm)
Xét hình 9a, phần hộp chứa sữa có dạng hình hộp chữ nhật với đáy là đáy của hộp sữa và chiều cao là 6 cm.
Do đó, trong hình 9a, phần hộp chứa sữa chiếm 6 phần, phần không chứa sữa chiếm 5 phần, thể tích cả hộp là: 5+6 = 11 phần.
Như vậy, tỉ số của của thể tích sữa có trong hộp và thể tích của cả hộp là \(\frac{6}{{11}}\).
CM
5 tháng 10 2018
Đáp án C
Gọi chiều dài đáy là x và chiều cao của hộp là y x ; y > 0 ; c m
Ta có
V = x 2 y = 180 ; S t p = 4 x y + 2 x 2 = 4.180 x + 2 x 2 = 360 x + 360 x + 2 x 2 ≥ 3 360 2 .2 3
Dấu “=” xảy ra
⇔ 360 x = 2 x 2 ⇔ x = 180 3 ⇒ y = 180 x 2 = 180 3 c m
CM
15 tháng 4 2017
Đáp án C
Gọi chiều dài đáy là x và chiều cao hộp là y (x, y > 0; cm)
Ta có
NM
Nguyễn Minh Quang
Giáo viên
1 tháng 6 2021
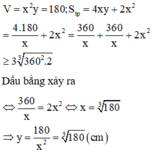
Gọi R là bán kính đáy hộp sữa
\(\Rightarrow\)chiều cao hộp sữa là : \(3R\)
Thể tích hộp sữa là : \(\pi R^2\times3R=192\pi\Leftrightarrow R^3=64\Leftrightarrow R=4cm\)
Ơ mà sao lại hỏi thể tích nhỉ, đề cho luôn là \(192\pi cm^3\) mà nhỉ
12 tháng 11 2021
Đổi: \(387g=0,387kg\)
\(V=0,314l=0,314dm^3=3,14\cdot10^{-4}\left(m^3\right)\)
a)Trọng lượng của hộp sữa:
\(P=10m=10\cdot0,387=3,87N\)
b)Trọng lượng riêng của sữa:
\(d=\dfrac{P}{V}=\dfrac{3,87}{3,14\cdot10^{-4}}=12324,84076\)(N/m3)
Khối lượng riêng:
\(d=10D\Rightarrow D=\dfrac{d}{10}=1232,484076\)(kg/m3)
TH
7 tháng 3 2022
Thể tích hình hộp chữ nhật là:
4,6 x 3,6 x 12 = 198,72(cm³)
Đáp số: 198,72 cm³
LM
Lê Minh Vũ
CTVHS
17 tháng 7 2023
Diện tích xung quanh của hộp sữa là:
\(\left(4+5\right)\times2\times12=216\left(cm^2\right)\)
Thể tích của hộp sữa là:
\(4\times5\times12=240\left(cm^3\right)\)
