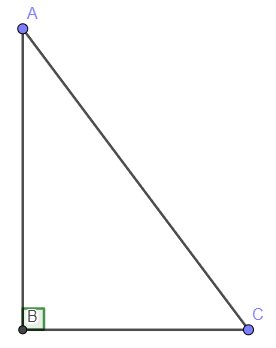
Cho ∆ABC vuông tại A. a) Biết AC = 5cm, AC = 12cm. Giải tam giác vuông ABC. b) Biết AC = 5cm, góc B = 40°. Giải tam giác vuông ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: AB=10cm
\(BC=5\sqrt{3}\left(cm\right)\)
\(\widehat{C}=60^0\)


a, \(sin\left(A\right)=\dfrac{BC}{AC}\Leftrightarrow sin\left(40^o\right)=\dfrac{BC}{8}\Leftrightarrow BC\approx5,14\left(cm\right)\)
\(cos\left(A\right)=\dfrac{AB}{AC}\Leftrightarrow cos\left(40^o\right)=\dfrac{AB}{8}\Leftrightarrow AB\approx6,12\left(cm\right)\)
b,
\(cotg\left(C\right)=\dfrac{BC}{AB}\Leftrightarrow\dfrac{1}{\sqrt{3}}=\dfrac{BC}{5}\Leftrightarrow BC=\dfrac{5\sqrt{3}}{3}\left(cm\right)\)
\(AC^2=AB^2+BC^2\Leftrightarrow AC=\sqrt{AB^2+BC^2}=\sqrt{5^2+\left(\dfrac{5\sqrt{3}}{3}\right)^2}=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)

a.
Xét tam giác ABC vuông tại A, có:
AB^2 + AC^2 = BC^2 (Định Lý Pytago) => BC^2 = 25+144 = 169
=> BC = 13 (cm)
sinB = AC/BC = 12/13 => B = 67.4 (độ)

bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ

A) tam giác ABH vuông tại A . Theo định lí Py-Ta Go ta có
\(AH^2+BH^2=AB^2\)
THAY BH = 5CM , AH = 12 CM , ta được
\(12^2+5^2=AB^2\)
\(AB^2\)= 144+25 =169
AB =\(\sqrt{169}\)=13 CM
SORRY MÌNH CHỈ GIẢI ĐƯỢC CÂU A THÔI
MONG BẠN THÔNG CẢM
a, Xét tam giác AHB, có ^AHB = 900
Áp dụng định lí Py ta go ta có :
\(AB^2=AH^2+HB^2=144+25=169\)
\(\Rightarrow AB^2=169\Rightarrow AB=13\)cm
b, Xét tam giác ACH, có ^AHC = 900
Áp dụng định lí Py ta go ta có :
\(AC^2=AH^2+CH^2\Rightarrow CH^2=AC^2-AH^2\)
\(=400-144=256\Rightarrow CH=\sqrt{256}=16\)cm
Vậy BC = CH + HB = 16 + 5 = 21 cm
Chu vi tam giác ABC là :
\(P_{\Delta ABC}=20+21+13=54\)cm


a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=5^2+12^2=169\)
=>\(BC=\sqrt{169}=13\left(cm\right)\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{5}{13}\)
nên \(\widehat{B}\simeq23^0\)
Ta có: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{C}\simeq90^0-23^0=67^0\)
b: Ta có: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{C}=90^0-40^0=50^0\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)
=>\(BC=\dfrac{AC}{sinB}=\dfrac{5}{sin40}\simeq7,78\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AB^2=BC^2-AC^2\)
=>\(AB\simeq\sqrt{7,78^2-5^2}\simeq5,96\left(cm\right)\)