Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Để hàm số là hàm số bậc nhất thì 2m-3<>0
hay m<>3/2
b: Để hàm số đồng biến thì 2m-3>0
hay m>3/2
Để hàm số nghịch biến thì 2m-3<0
hay m<3/2
c: Thay x=1 và y=-4 vào (d), ta được:
\(m-1+m+3=-4\)
\(\Leftrightarrow2m=-6\)
hay m=-3
a: Thay x=-2 và y=6 vào (d), ta được:
-2a+4=6
=>-2a=2
=>a=2/-2=-1
b: a=-1 nên \(y=-x+4\)
Khi m = 2 : y = x + 5
TXĐ : D = R.
Tính biến thiên :
bảng biến thiên :
x | -∞ | +∞ | |
y | -∞ |
| +∞ |
Bảng giá trị :
x | 0 | -5 |
y | 5 | 0 |
Đồ thị hàm số y = x + 5 là đường thẳng đi qua hai điểm A(0, 5) và B(-5; 0).
b/(dm) đi qua điểm A(4, -1) :
4 = (m -1)(-1) +2m +1
<=> m = 2
3. hàm số nghịch biến khi : a = m – 1 < 0 <=> m < 1
4.(dm) đi qua điểm cố định M(x0, y0) :
Ta được : y0 = (m -1)( x0) +2m +1 luôn đúng mọi m.
<=> (x0 + 2) m = y0 – 1 + x0(*)
(*) luôn đúng mọi m khi :
x0 + 2= 0 và y0 – 1 + x0 = 0
<=> x0 =- 2 và y0 = 3
Vậy : điểm cố định M(-2, 3)
a: Thay x=2 và y=-3 vào (d), ta được:
\(2\left(2m-1\right)-2m+5=-3\)
=>\(4m-2-2m+5=-3\)
=>2m+3=-3
=>2m=-6
=>\(m=-\dfrac{6}{2}=-3\)
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}2m-1=2\\-2m+5\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m=3\\-2m\ne-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m\ne2\end{matrix}\right.\)
=>m=3/2
Thay m=3/2 vào (d), ta được:
\(y=\left(2\cdot\dfrac{3}{2}-1\right)x-2\cdot\dfrac{3}{2}+5=2x+2\)
y=2x+2 nên a=2
Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
\(tan\alpha=2\)
=>\(\alpha\simeq63^026'\)
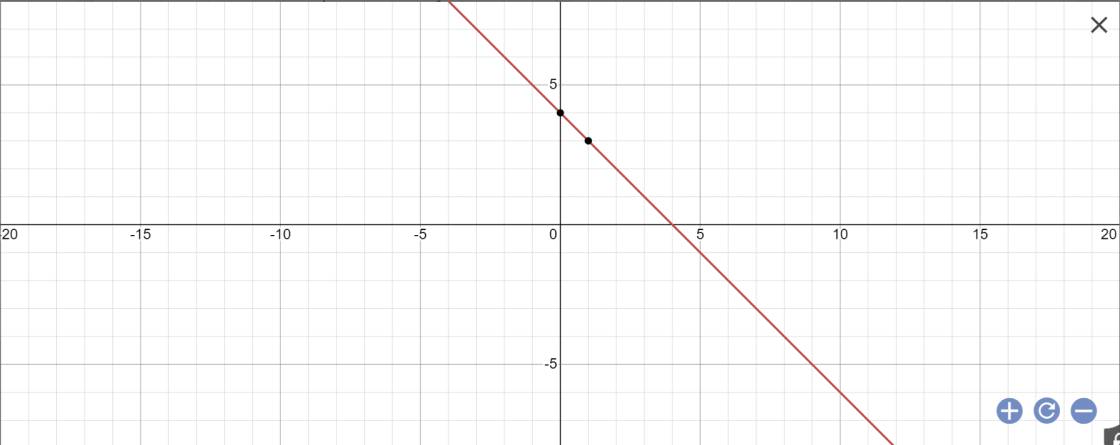
Lời giải:
a. Vì $(d)$ đi qua $M(3;1)$ nên:
$y_M=(2-a)x_M+a$
$\Leftrightarrow 1=(2-a).3+a\Rightarrow a=2,5$
Khi đó: $y=(2-2,5)x+2,5=-0,5x+2,5$
Vì $-0,5<0$ nên hàm nghịch biến trên R.
b.
$y_A=3$
$-0,5x_A+2,5=-0,5.(-1)+2,5=3$
$\Rightarrow y_A=-0,5x_A+2,5$ nên điểm $A\in (d)$
c. Gọi PTĐT $(d')$ là: $y=mx+n$ với $m,n$ là số thực
$(d')\parallel (d)$ nên $m=-0,5$
$M(3;1), N(-1,5)\Rightarrow$ tọa độ trung điểm $I$ của $MN$ là:
$(\frac{3-1}{2}; \frac{1+5}{2})=(1,3)$
$(d')$ đi qua $(1,3)$ nên:
$3=m.1+n\Rightarrow m+n=3\Rightarrow n=3-m=3-(-0,5)=3,5$
Vậy PTĐT $(d')$ là: $y=-0,5x+3,5$