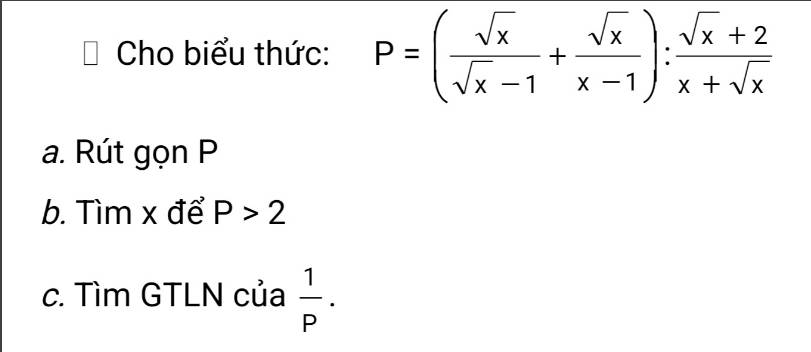Nhờ mn giúp em vs ạ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét (O) có
ΔABN nội tiếp
AB là đường kính
Do đó: ΔABN vuông tại N
=>AN\(\perp\)NB tại N
=>BN\(\perp\)AM tại N
Xét (O) có
ΔAHB nội tiếp
AB là đường kính
Do đó: ΔAHB vuông tại H
=>AH\(\perp\)HB tại H
=>BH\(\perp\)AD tại H
Xét ΔBAM vuông tại B có BN là đường cao
nên \(AN\cdot AM=AB^2\left(1\right)\)
Xét ΔABD vuông tại B có BH là đường cao
nên \(AH\cdot AD=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AN\cdot AM=AH\cdot AD\)
c: ta có: ΔOAN cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)AN
Xét ΔIAO vuông tại I và ΔNBM vuông tại N có
\(\widehat{IAO}=\widehat{NBM}\left(=90^0-\widehat{AMB}\right)\)
Do đó: ΔIAO~ΔNBM
Xét tứ giác OIMB có
\(\widehat{OBM}+\widehat{OIM}=90^0+90^0=180^0\)
nên OIMB là tứ giác nội tiếp
=>\(\widehat{MOB}=\widehat{MIB}\)
Xét ΔOBM vuông tại B và ΔINB vuông tại N có
\(\widehat{BOM}=\widehat{NIB}\left(cmt\right)\)
Do đó: ΔOBM~ΔINB

a: \(3x-12-4\sqrt{x}+8=6\sqrt{2x+1}-18\)
=>\(\left(x-4\right)\cdot3-4\left(\sqrt{x}-2\right)=6\left(\sqrt{2x+1}-3\right)\)
=>\(3\left(x-4\right)-\dfrac{4\left(x-4\right)}{\sqrt{x}+2}-6\cdot\dfrac{2x+1-9}{\sqrt{2x+1}+3}=0\)
=>\(\left(x-4\right)\left(3-\dfrac{4}{\sqrt{x}+2}-\dfrac{12}{\sqrt{2x+1}+3}\right)=0\)
=>x-4=0
=>x=4
b: \(\Leftrightarrow\sqrt{x^2+x-1}-1+\sqrt{x-x^2+1}-1=x^2-x\)
=>\(\dfrac{x^2+x-1-1}{\sqrt{x^2+x-1}+1}+\dfrac{x-x^2+1-1}{\sqrt{x-x^2+1}+1}=x\left(x-1\right)\)
=>\(\dfrac{\left(x+2\right)\left(x-1\right)}{\sqrt{x^2+x-1}+1}-\dfrac{x\left(x-1\right)}{\sqrt{x-x^2+1}+1}-x\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(\dfrac{x+2}{\sqrt{x^2+x-1}+1}-\dfrac{x}{\sqrt{x-x^2+1}+1}-x\right)=0\)
=>x-1=0
=>x=1
c: \(\Leftrightarrow x^2-\sqrt{x^3-x^2}-\sqrt{x^2-x}=0\)
=>\(\sqrt{x}\left(x\sqrt{x}-\sqrt{x^2-x}-\sqrt{x-1}\right)=0\)
=>căn x=0
=>x=0

Bài 3:
b: Gọi K là giao điểm của AB và OP
Xét (O) có
PA,PB là các tiếp tuyến
Do đó: PA=PB
=>P nằm trên đường trung trực của BA(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(2)
Từ (1) và (2) suy ra PO là đường trung trực của AB
=>PO\(\perp\)AB tại K và K là trung điểm của AB
Ta có: ΔOAP vuông tại A
=>\(AP^2+AO^2=OP^2\)
=>\(AP^2=OP^2-OA^2=d^2-R^2\)
=>\(AP=\sqrt{d^2-R^2}\)
Xét ΔOAP vuông tại A có AK là đường cao
nên \(AK\cdot OP=AO\cdot AP\)
=>\(AK\cdot d=R\cdot\sqrt{d^2-R^2}\)
=>\(AK=\dfrac{R\cdot\sqrt{d^2-R^2}}{d}\)
K là trung điểm của AB
=>\(AB=2\cdot AK=\dfrac{2\cdot R\cdot\sqrt{d^2-R^2}}{d}\)
Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>\(BA^2+AC^2=BC^2\)
=>\(AC^2=\left(2R\right)^2-\left(\dfrac{2R\sqrt{d^2-R^2}}{d}\right)^2\)
=>\(AC^2=4R^2-\dfrac{4R^2\cdot\left(d^2-R^2\right)}{d^2}\)
=>\(AC^2=\dfrac{4R^2d^2-4R^2\left(d^2-R^2\right)}{d^2}=\dfrac{4R^4}{d^2}\)
=>\(AC=\dfrac{2R^2}{d}\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AC\cdot AB\)
=>\(AH\cdot2R=\dfrac{2R^2}{d}\cdot\dfrac{2R\sqrt{d^2-R^2}}{d}\)
=>\(AH=\dfrac{R\cdot2R\sqrt{d^2-R^2}}{d^2}=\dfrac{2R^2\cdot\sqrt{d^2-R^2}}{d^2}\)

1 I need to ask you some questions
4 If she weren't lazy, she could pass the exam
5 If she weren't shy, she would enjoy the party

\(n_{Fe}=a;n_{Cu}=b\\ 56a+64b=9,2\left(I\right)\\ BTe^{^{ }-}:3a+2b=2n_{SO_2}\left(II\right)\\ n_{H_2SO_4pư}=n_{SO_2}+1,5a+b\\ n_{H_2SO_4sau}=\dfrac{50.0,98}{98}-n_{SO_2}-1,5a-b=0,5-n_{SO_2}-1,5a-b\\ m_{ddsau}=9,2+50-64n_{SO_2}=59,2-64n_{SO_2}\\ \Rightarrow:\dfrac{98\left(0,5-n_{SO_2}-1,5a-b\right)}{59,2-64n_{SO_2}}=\dfrac{30,625}{100}\left(III\right)\\ \Rightarrow a=0,05;b=0,1;n_{SO_2}=0,175mol\\ V=0,175.22,4=3,92L\\ \%m_{Fe}=\dfrac{0,05.56}{9,2}.100\%=30,43\%\\ \%m_{Cu}=69,57\%\)

Lời giải:
a. ĐKXĐ: $x>0; x\neq 1$
\(P=\left[\frac{\sqrt{x}(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{x}+1)}+\frac{\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}\right].\frac{x+\sqrt{x}}{\sqrt{x}+2}\)
\(=\frac{x+\sqrt{x}+\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}.\frac{\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}+2}=\frac{\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}-1)(\sqrt{x}+1)}.\frac{\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}+2}=\frac{x}{\sqrt{x}-1}\)
b.
$P>2 \Leftrightarrow \frac{x}{\sqrt{x}-1}-2>0$
$\Leftrightarrow \frac{x-2\sqrt{x}+2}{\sqrt{x}-1}>0$
$\Leftrightarrow \frac{(\sqrt{x}-1)^2+1}{\sqrt{x}-1}>0$
$\Leftrightarrow \sqrt{x}-1>0$ (do $(\sqrt{x}-1)^2+1>0$)
$\Leftrightarrow x>1$
Kết hợp đkxđ suy ra $x>1$
c.
$\frac{1}{P}=\frac{\sqrt{x}-1}{x}$
Áp dụng BĐT Cô-si:
$x+4\geq 4\sqrt{x}\Rightarrow x\geq 4(\sqrt{x}-1)$
$\Rightarrow \frac{\sqrt{x}-1}{x}\leq \frac{\sqrt{x}-1}{4(\sqrt{x}-1)}=\frac{1}{4}$
Vậy $\frac{1}{P}$ max $=\frac{1}{4}$ khi $x=4$


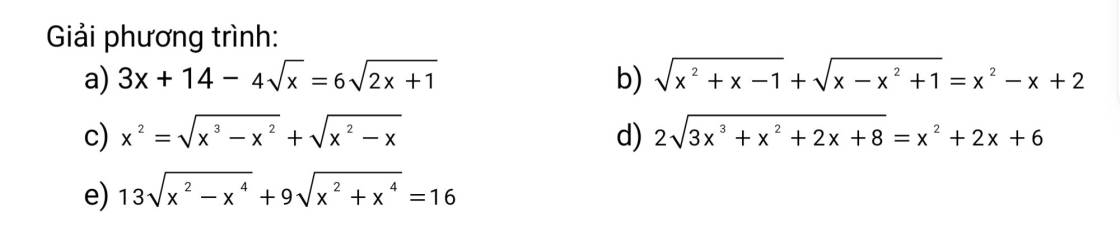 Nhờ mn giúp em vs ạ. c.ơn nhìu
Nhờ mn giúp em vs ạ. c.ơn nhìu


 Nhờ mn giúp mik vs ạ
Nhờ mn giúp mik vs ạ