Cho tam giác ABC nhọn , đường thẳng song song với BC cắt các cạnh AB và AC theo thứ tự ở D và E
a) Tính độ dài AB biết AE/EC = 3/4 , DB = 8cm
b) AD/DB=EC/AE . C/m D,E theo thứ tự là trung điểm AB và AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

AD=6,8-4=2,8cm
DE//BC
=>AE/EC=AD/DB
=>4,2/EC=2,8/4=7/10
=>EC=6cm

a) Theo bài ra ta có:\(\frac{AE}{EC}=\frac{3}{4}\)=> \(\frac{AE}{EC+AE}=\frac{3}{4+3}\Rightarrow\frac{AE}{AC}=\frac{3}{7}\)
Xét ΔABC có DE//BC => \(\frac{DE}{BC}=\frac{AE}{AC}=\frac{3}{7}\) (hệ quả đ/lí Ta-lét)
=> DE = \(\frac{3}{7}BC=\frac{3}{7}.28=12\left(cm\right)\)
b) Xét ΔABC có DE//BC => \(\frac{AD}{BD}=\frac{AE}{EC}\) (đ/lí Ta-lét)
Mà \(\frac{AD}{BD}=\frac{EC}{AE}\left(gt\right)\) => \(\frac{AE}{EC}=\frac{EC}{AE}\) (=\(\frac{AD}{BD}\))
=>AE2=EC2 => AE = EC
=> E là trung điểm của AC.
Xét ΔABC có: DE//BC ; E là trung điểm của AC (cmt)
=> D là trung điểm của AB
Chúc bạn học tốt!

Do DE song song BC
=> Theo định lý Talet, DA/DB = EA/EC
Mà DA/DB= EC/EA
=> EC=EA
=> E là trung điểm AC
=> DE là đường trung bình của tam giác ABC
=> D cũng là trung điểm AB

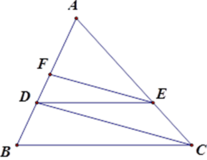
Áp dụng định lý Ta-lét:
Với EF // CD ta có A F A D = A E A C
Với DE // BC ta có A E A C = A D A B
Suy ra A F A D = A D A B , tức là A F . A B = A D 2
Vậy 9.16 = A D 2 ó A D 2 = 144 ó AD = 12
Đáp án: C
a: Xét ΔABC có DE//BC
nên \(\dfrac{AE}{EC}=\dfrac{AD}{DB}\)
=>\(\dfrac{AD}{8}=\dfrac{3}{4}\)
=>\(AD=8\cdot\dfrac{3}{4}=6\left(cm\right)\)
AB=BD+AD
=6+8
=14(cm)
b: Xét ΔABC có DE//BC
nên \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
mà \(\dfrac{AD}{DB}=\dfrac{EC}{AE}\)
nên \(\dfrac{AE}{EC}=\dfrac{EC}{AE}\)
=>\(AE^2=EC^2\)
=>AE=EC
=>E là trung điểm của AC
Xét ΔABC có
E là trung điểm của AC
ED//BC
Do đo: D là trung điểm của AB