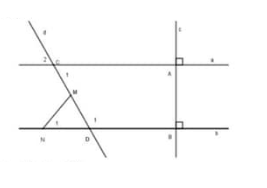
cho hình vẽ sau, chứng minh a//b và tính số đo của K2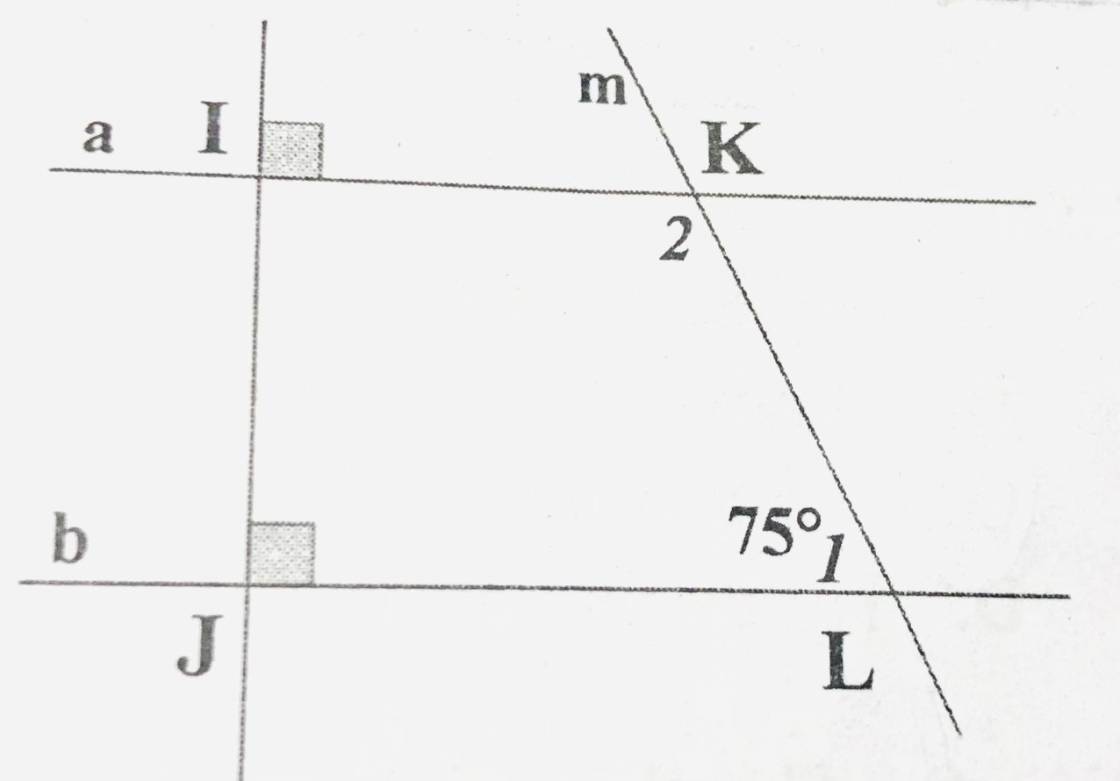
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Do \(\widehat{ABD}\) đổi đỉnh với góc bên ngoài
\(\Rightarrow\widehat{ABD}=75^o\)
b) Ta có \(\widehat{ABd}=180^o-75^o=105^o\) (kể bù)
\(\Rightarrow\widehat{\text{C}DB}=\widehat{ABd}=105^o\)
Mà hai góc này ở vị trí đồng vị
\(\Rightarrow a//b\)
d) Ta có: \(a//b\) và \(a\perp c\)
\(\Rightarrow b\perp c\)
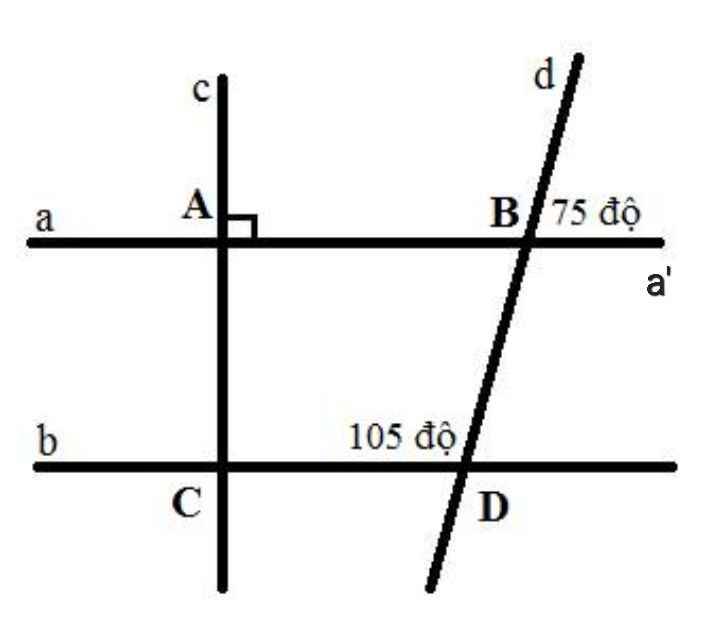 a) Do ∠ABD và ∠dBa' là hai góc đối đỉnh
a) Do ∠ABD và ∠dBa' là hai góc đối đỉnh
⇒ ∠ABD = ∠dBa' = 75⁰
b) Ta có:
∠ABD + ∠a'BD = 180⁰ (kề bù)
⇒ ∠a'BD = 180⁰ - ∠ABD
= 180⁰ - 75⁰
= 105⁰
⇒ ∠a'BD = ∠CDB = 105⁰
Mà ∠a'BD và ∠CDB là hai góc so le trong
⇒ a // b
c) Do c ⊥ a (gt)
a // b (cmt)
⇒ c ⊥ b

a: Ta có: AC\(\perp\)AB
BD\(\perp\)AB
Do đó: AC//BD
b: bạn vẽ lại hình nha bạn

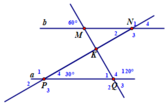
a. Q ^ 1 = 60 ° ( kề bù với Q ^ 4 ) mà Q 1 ^ đồng vị với M ^ = 60 ° => a//b
b. Vì a//b N 4 ^ = P ^ 4 = 30 ° ( đồng vị) ⇒ N ^ 1 = N ^ 3 = 150 ° ⇒ N ^ 4 = N ^ 2 = 130 °

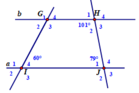
a. H 2 ^ + J 1 ^ = 101 ° + 79 ° mà 2 góc này ở vị trí trong cùng phía => a // b
b. a / / b ⇒ G 4 ^ = I 4 ^ (đồng vị) ⇒ G ^ 1 = G 3 ^ = 120 ° ; G ^ 4 = G ^ 2 = 60 °
 đây bạn ơi giúp mik nha
đây bạn ơi giúp mik nha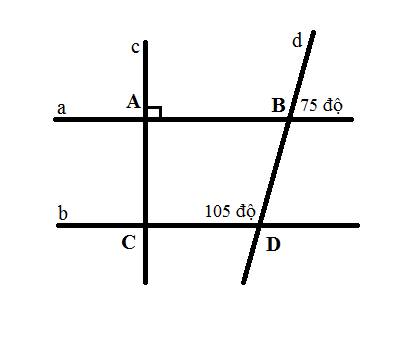

 a.
a.
a \(\perp\) IJ
b \(\perp\) IJ
⇒ a//b (Vì trong cùng một mặt phẳng hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
\({}\) \(\widehat{K_2}\) + \(\widehat{L_1}\)= 1800 (hai góc trong cùng phía có tổng bằng 1800)
\(\widehat{K_2}\) + \(\widehat{L_1}\)= 1800 (hai góc trong cùng phía có tổng bằng 1800)
\({}\) \(\widehat{K_2}\) = 1800 - 750
\(\widehat{K_2}\) = 1800 - 750
\({}\) \(\widehat{K_2}\) = 1050
\(\widehat{K_2}\) = 1050