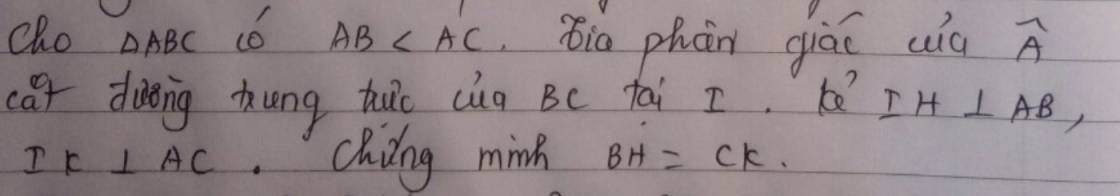 vẽ hình cho mik luôn nhé
vẽ hình cho mik luôn nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\widehat{ACB}=90^0-60^0=30^0\)
b: Xét ΔABH và ΔKBH có
BA=BK
BH chung
AH=KH
Do đó: ΔABH=ΔKBH
Ta có: ΔABK cân tại B
mà BI là đường trung tuyến
nên BI là đường cao

chưa vẽ được
tick cho mình cái
Bài tập 1
a) Chứng minh AFOE cân
Xét tam giác AOB và tam giác FOE, ta có:
Do đó, hai tam giác AOB và FOE đồng dạng theo tỉ số 1:1.
Vậy, AFOE cân tại F.
b) Trên tia đối của tòa FB lấy điểm 1 sao cho F1 = FB. Chứng minh OF = h OE == DI
Xét tam giác F1OB và tam giác FOE, ta có:
Do đó, hai tam giác F1OB và FOE đồng dạng theo tỉ số 1:1.
Vậy, OF = OE = DI.
c) Gia sư BAD =50. Tính EOF
Xét tam giác EOF, ta có:
Do đó, EOF = 25^2 = 625.
Kết luận
Bài tập 2
Chứng minh 1 đổi xứng với K qua Đ
Xét tam giác AFE và tam giác BKF, ta có:
Do đó, hai tam giác AFE và BKF đồng dạng theo tỉ số 1:1.
Vậy, I đối xứng với K qua D.
Kết luận
I đối xứng với K qua D.
Bài tập 3
Chứng minh Nạp là hai điểm đối xứng nhau qua ở
Xét tam giác MNO và tam giác MNP, ta có:
Do đó, hai tam giác MNO và MNP đồng dạng theo tỉ số 1:1.
Vậy, N và P là hai điểm đối xứng nhau qua O.
Kết luận
N và P là hai điểm đối xứng nhau qua O.
Chúc bạn học tốt!

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>AD=ED
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc EBF chung
=>ΔBEF=ΔBAC
=>BF=BC
2BF=BF+BC>FC

a. \(A\left(2:-3\right)\in\left(d\right)\Rightarrow-3=4m-2+2m+5\)
\(\Rightarrow m=\dfrac{3}{2}\)
\(3.y=\left(2m-1\right)x-2m+5\left(m\ne\dfrac{1}{2}\right)\)
\(\left(2;-3\right)\in\left(d\right)\Rightarrow-3=\left(2m-1\right).2-2m+5\Leftrightarrow m=-3\left(tm\right)\)
\(b,\left(d\right)//\left(d'\right)\Rightarrow\left\{{}\begin{matrix}2m-1=2\\-2m+5\ne1\\\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=1,5\left(tm\right)\\m\ne2\end{matrix}\right.\)
\(\Rightarrow\left(d\right):y=2x+2\)\(đi-qua-A\left(0;2\right),B\left(-1;0\right)\Rightarrow\cos\left(\alpha\right)=\dfrac{\left|OB\right|}{\left|OA\right|}=\dfrac{\left|-1\right|}{2}\Rightarrow\alpha=60^o\)
\(c,gọi-điểm-cố-định-làC\left(xo;yo\right)\Rightarrow\left(2m-1\right)xo-2m+5=yo\)
\(\Leftrightarrow2mxo-xo-2m+5-yo=0\)
\(\Leftrightarrow2m\left(xo-1\right)-xo-yo+5=0\Rightarrow\left\{{}\begin{matrix}xo=1\\yo=4\end{matrix}\right.\)
\(\Rightarrow C\left(1;4\right)là-điểm-cố-định\)
\(\)

a) Vì tia ON là tia phân giác của góc AOC: góc NOC = góc AON = góc AOC : 2 = 150 độ : 2 = 75 độ.
Vì tia OM là tia phân giác của góc AOB nên: góc AOM = góc MOB = góc AOB : 2 = 50 độ : 2 = 25 độ.
Trên cùng một nửa mặt phẳng bờ chứa tia OA ta có: góc AON = 75 độ góc AOM = 25 độ ⇒ Góc AON > góc AOM ⇒ Tia OM nằm giữa hai tia OA và ON.
⇒ Góc AOM + góc MON = góc AON 25 độ + góc MON = 75 độ góc MON = 75 độ - 25 độ góc MON = 50 độ
b) Trên cùng một nửa mặt phẳng bờ chứa tia OM ta có: Góc MON = 50 độ Góc MOB = 25 độ ⇒ Góc MON > góc MOB ⇒ Tia OB nằm giữa hai tia OM và ON.
⇒ Góc MOB + góc BON = góc MON ⇒ 25 độ + góc BON = 50 độ ⇒ góc BON = 50 độ - 25 độ ⇒ góc BON = 25 độ
Ta có: Góc BON = góc MOB (= 25 độ) Tia OB nằm giữa hai tia OM và ON. ⇒ Tia OB là tia phân giác của góc MON.
Lời giải:
Vì $I$ nằm trên đường trung trực của $BC$ nên $BI=CI$
Vì $I$ nằm trên đường phân giác $\widehat{BAC}$ nên khoảng cách từ $I$ đến $AB$ bằng khoảng cách từ $I$ đến $AC$
$\Rightarrow IH=IK$
Xét tam giác vuông $IHB$ và $IKC$ có:
$IH=IK$ (cmt)
$IB=IC$ (cmt)
$\Rightarrow \triangle IHB=\triangle IKC$ (ch-gn)
$\Rightarrow HB=KC$ (đpcm)
Hình vẽ: