K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
0
Những câu hỏi liên quan
1 tháng 4 2023
a: \(\dfrac{a}{b}+\dfrac{b}{a}>=2\cdot\sqrt{\dfrac{a}{b}\cdot\dfrac{b}{a}}=2\)
b: a<b
=>-2a>-2b
=>-2a-3>-2b-3
c: =x^2+2xy+y^2+y^2+6y+9
=(x+y)^2+(y+3)^2>=0 với mọi x,y
d: a+3>b+3
=>a>b
=>-5a<-5b
=>-5a+1<-5b+1
HD
9 tháng 3 2022
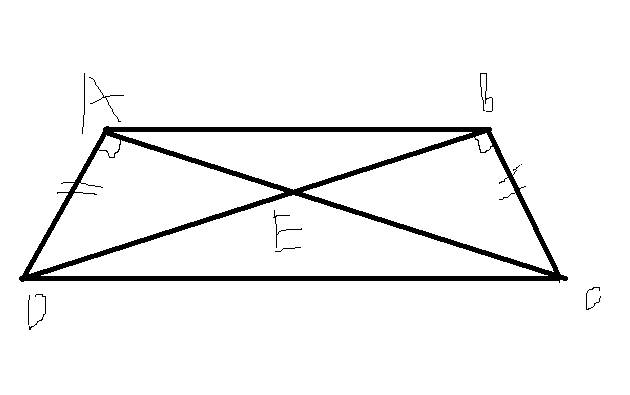
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
ˆBADBAD^ chung
Do đó: ΔADB=ΔAEC
b: Ta có: ΔADB=ΔAEC
nên BD=CE
Xét ΔEBC vuông tạiE và ΔDCB vuông tại D có
BC chung
CE=BD
Do đó:ΔEBC=ΔDCB
Suy ra: ˆOCB=ˆOBCOCB^=OBC^
hay ΔOBC cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
d: Ta có: ΔEBC vuông tại E
mà EM là đường trung tuyến
nên BC=2EM
17 tháng 8 2023
a: Xét ΔADC vuông tại A và ΔBCD vuông tại B có
AD=BC
DC chung
=>ΔADC=ΔBCD
b: ΔADC=ΔBCD
=>góc ACD=góc BDC
=>góc EDC=góc ECD
=>ΔEDC cân tại E
c: Xét ΔEAD vuông tại A và ΔEBC vuông tại B có
ED=EC
AD=BC
=>ΔEAD=ΔEBC
=>EA=EB
Xét ΔEAB và ΔECD có
EA/EC=EB/ED
góc AEB=góc CED
=>ΔEAB đồng dạng với ΔECD
=>góc EAB=góc ECD
=>AB//CD
TD
3 tháng 2 2022
=)) Yêu cầu vẽ gì ở đề bài với câu b v bạn cm gì ở phần a v đăng lại bài đi
.
BC.
17 tháng 6 2023
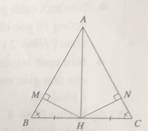
b: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc BAE chung
=>ΔABE đồng dạng vớiΔACF
=>AB/AC=AE/AF
=>AB*AF=AC*AE
c: XétΔABC có
BE,CF là đường cao
BE cắt CF tại H
=>H là trực tâm
=>AH vuông góc BC
PP
1
10 tháng 9 2021
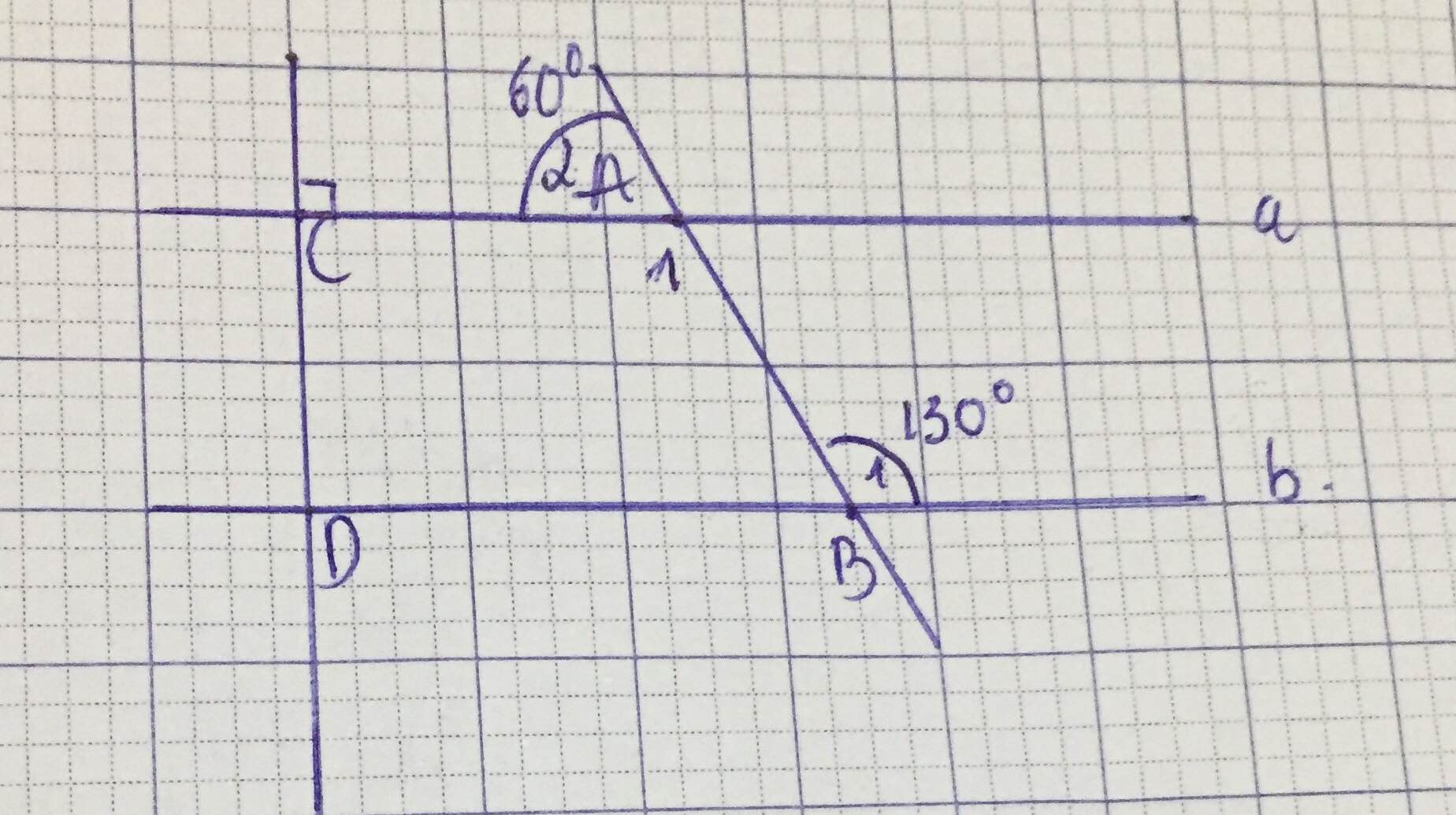
\(a,\) Muốn chứng minh \(a//b\) thì bạn phải sửa \(\widehat{B_1}=120\) nha
Ta có \(\widehat{A_1}+\widehat{A_2}=180\left(kề.bù\right)\Rightarrow\widehat{A_1}=180-\widehat{A_2}=120\)
Mà \(\widehat{B_1}=120\Rightarrow\widehat{A_1}=\widehat{B_1}\left(=120\right)\)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow a//b\)
\(b,\left\{{}\begin{matrix}a\perp c\left(GT\right)\\a//b\left(cmt\right)\end{matrix}\right.\Rightarrow b\perp c\)