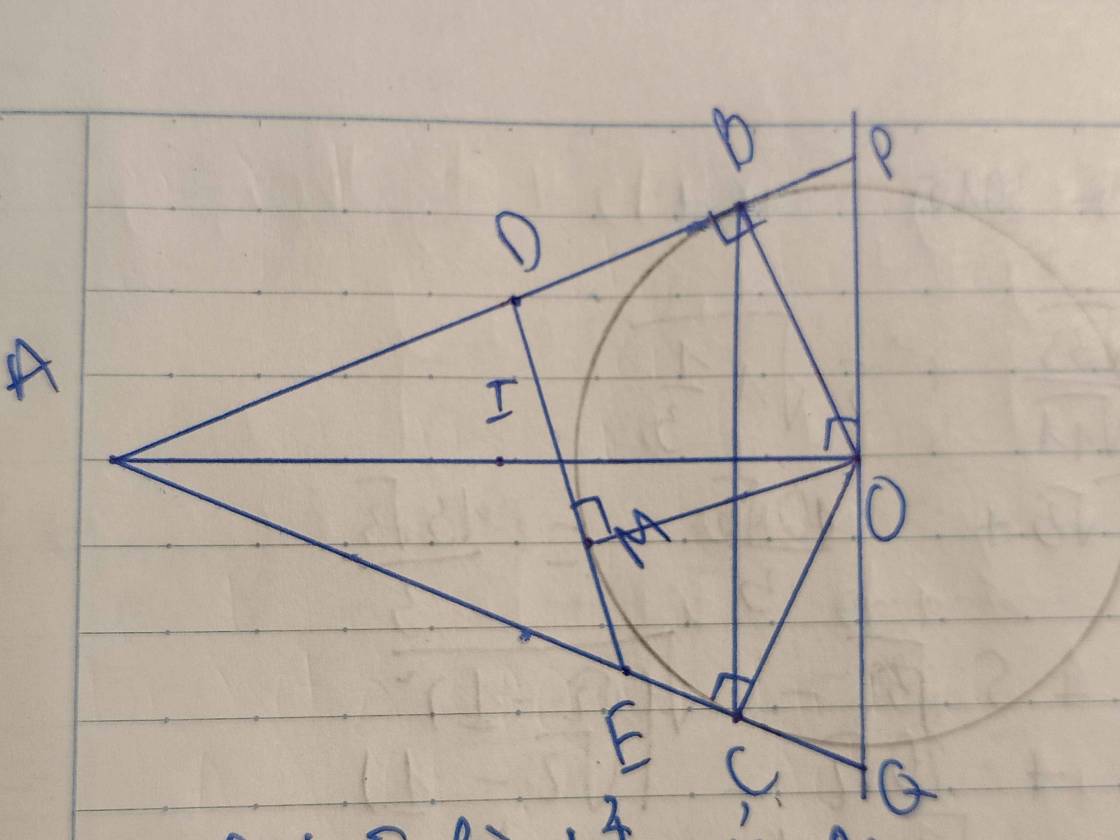
 Cho điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB,AC với đường tròn (O) (B,C là các tiếp điểm)
Cho điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB,AC với đường tròn (O) (B,C là các tiếp điểm)
a, Chứng minh 4 điểm A,B,O,C thuộc một đường tròn
b. Trên cung nhỏ BC của (O) lấy điểm M ( M khác B, M khác C, M khác AO). Tiếp tuyến tại M cắt AB,AC lần lượt tại D và E. Chứng minh chu vi tam giác ADE=2AB
c, Đường thẳng vuông góc với AO tại O cắt AB và AC lần lượt tại P và Q. Chứng minh 4PO.QE=PQ²
Các a/chị ơi, e đang thắc mắc ở câu c ạ, hai câu a và b thì e đã có cách làm rồi ạ. Cảm ơn a/chị thật nhiều ạ

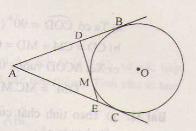
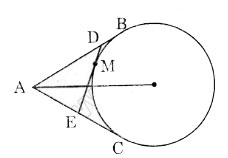
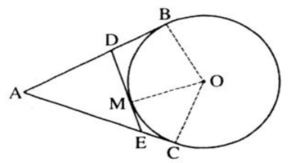
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
DB,DM là các tiếp tuyến
Do đó: DB=DM
Xét (O) có
EM,EC là các tiếp tuyến
Do đó: EM=EC
Chu vi tam giác ADE là:
\(C_{ADE}=AD+DE+AE\)
\(=AD+DM+ME+AE\)
\(=AD+DB+CE+AE\)
\(=AB+AC=2\cdot AB\)