So sánh s1 và s2
s1:2+4+6+...+5000
s2:2.2.5.5.5.5.2051
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LM
0
4 tháng 4 2021
uses crt;
const s1='Pin_NLMT';
s2='Pin_luthium';
s3='Pin_JA_Solar';
s4='Pin_Jinko_Solar';
begin
clrscr;
if s1<s4 then writeln('Xau s1 nho hon xau s4')
else if s1=s4 then writeln('Xau s1 bang xau s4)
else writeln('Xau s1 lon hon xau s4');
if s2<s3 then writeln('Xau s2 nho hon xau s3')
else if s2=s3 then writeln('Xau s2 bang xau s3')
else writeln('Xau s2 lon hon xau s3');
readln;
end.
HD
1
ND
1
DD
Đoàn Đức Hà
Giáo viên
7 tháng 2 2021
\(S_1=1+\left(-3\right)+5+\left(-7\right)+...+17\)
Số số hạng của tổng trên là: \(\frac{17-1}{2}+1=9\)
\(S_1=1+\left[-3+5\right]+\left[-7+9\right]+...+\left[-15+17\right]\)
\(S_1=1+2+2+2+2=9\)
\(S_2=-2+4+\left(-6\right)+8+...+\left(-18\right)\)
Số số hạng của tổng trên là: \(\frac{18-2}{2}+1=9\)
\(S_2=\left(-2+4\right)+\left(-6+8\right)+...+\left(-18\right)\)
\(S_2=2+2+2+2-18=-10\)
18 tháng 1 2018
kết bạn nha
s1 = 1+ (-3) +5 +(-7)+....+17 = (1+5+..+13+17)-(3+7+...+15)
Áp dụng công thức : tổng dãy số cách đều = số số hạng . tổng số đầu và số cuối chia đôi
s2 tương tự
7 tháng 12 2017
S1+S2=(1-2-3+4)+(5-6-7+8)+(9-10-11+12)+(13-14-15+16)+17-18
= 0 + 0 + 0 + 0 +17-18
=-1
CM
24 tháng 5 2017
Chọn D.
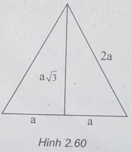
(h.2.60) Bán kính đáy của hình nón là a, đường sinh của hình nón là 2a.
Do đó, ta có:
S 1 = π Rl = π .a.2a = 2 πa 2 (1)
Mặt cầu có bán kính là a 3 /2, nên ta có:
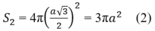
Từ (1) và (2) suy ra: 2 S 2 = 3 S 1