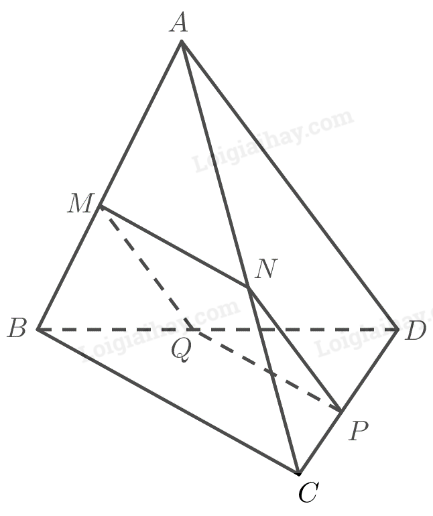
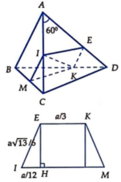
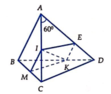
Cho tứ diện ABCD. Gọi K là điểm thuộc cạnh CD sao cho \(2KD=3KC\) và I là điểm thuộc đoạn thẳng BK sao cho \(IK=2IB\). Mặt phẳng \(\left(\alpha\right)\) đi qua I và luôn cắt các tia AB, AC, AD lần lượt tại các điểm M, N, P (khác đỉnh A). Tìm giá trị nhỏ nhất của biểu thức:
\(T=4.\dfrac{AB^2}{AM^2}+9.\dfrac{AC^2}{AN^2}+16.\dfrac{AD^2}{AP^2}\)