Với \(a\ge0,a\ne1\), chứng minh \(\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1-\sqrt{a}}{1-a}\right)^2=1\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 11 2021
Câu b bạn sửa lại đề
\(a,VT=\left[1+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\right]\left[1-\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}\right]\\ =\left(1+\sqrt{x}\right)\left(1-\sqrt{x}\right)=1-x=VP\\ b,VT=\dfrac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{ab}}+\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\\ =\sqrt{a}-\sqrt{b}+\sqrt{a}+\sqrt{b}=2\sqrt{a}=VP\)
13 tháng 11 2021
a: \(=\left(1+\sqrt{x}\right)\left(1-\sqrt{x}\right)=1-x\)
DP
17 tháng 2 2019
\(VT=\dfrac{\left(1-\sqrt{x}\right)\left(1+\sqrt{x}+x\right)}{1-\sqrt{x}}.\left(\dfrac{1-\sqrt{x}}{\left(1-\sqrt{x}\right)\left(1+\sqrt{x}\right)}\right)^2\)
\(=\left(1+\sqrt{x}+x\right).\left(\dfrac{1}{1+\sqrt{x}}\right)^2\)
\(=\left(1+\sqrt{x}+x\right).\dfrac{1}{\left(1+\sqrt{x}\right)^2}\)
\(=\dfrac{1+\sqrt{x}+x}{\left(1+\sqrt{x}\right)^2}=\dfrac{\left(1+\sqrt{x}\right)^2}{\left(1+\sqrt{x}\right)^2}=1=VP\)
AP
20 tháng 10 2018
Qua đây tham khảo nè bạn: https://loigiaihay.com/bai-75-trang-40-sgk-toan-9-tap-1-c44a26987.html
1 tháng 7 2019
\(\left(1+\frac{a+\sqrt{a}}{\sqrt{a}+1}\right).\left(1-\frac{a-\sqrt{a}}{\sqrt{a}-1}\right)=1-a\)
\(=[1+\frac{\sqrt{a}.\left(\sqrt{a}+1\right)}{\sqrt{a+1}}].[1-\frac{\sqrt{a}.\left(\sqrt{a}-1\right)}{\sqrt{a}-1}]\)
\(=\left(1+\sqrt{a}\right).\left(1-\sqrt{a}\right)\)
\(=1-a\)
30 tháng 7 2022
a: \(=x-\sqrt{xy}+y-x+2\sqrt{xy}-y=\sqrt{xy}\)
b: \(=\dfrac{1+\sqrt{a}}{a-\sqrt{a}}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\dfrac{\sqrt{a}-1}{\sqrt{a}}\)
6 tháng 8 2022
Câu 1:
a: \(Q=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{3}\)
\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
b: Để Q>0 thì \(\sqrt{a}-2>0\)
=>a>4
16 tháng 5 2023
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{2}{x+\sqrt{x}+1}\)
AH
Akai Haruma
Giáo viên
20 tháng 8 2023
Lời giải:
A có min thôi bạn nhé.
\(A=\frac{\sqrt{x}+1+\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}: \frac{\sqrt{x}-(\sqrt{x}-1)}{\sqrt{x}-1}\)
\(=\frac{2\sqrt{x}+1}{(\sqrt{x}-1)(\sqrt{x}+1)}:\frac{1}{\sqrt{x}-1}=\frac{2\sqrt{x}+1}{(\sqrt{x}-1)(\sqrt{x}+1)}.(\sqrt{x}-1)=\frac{2\sqrt{x}+1}{\sqrt{x}+1}\)
\(=\frac{2(\sqrt{x}+1)-1}{\sqrt{x}+1}=2-\frac{1}{\sqrt{x}+1}\)
Vì $\sqrt{x}\geq 0$ với mọi $x\geq 0; x\neq 1$ nên $\sqrt{x}+1\geq 1$
$\Rightarrow \frac{1}{\sqrt{x}+1}\leq 1$
$\Rightarrow A=2-\frac{1}{\sqrt{x}+1}\geq 2-1=1$
Vậy $A_{\min}=1$ tại $x=0$
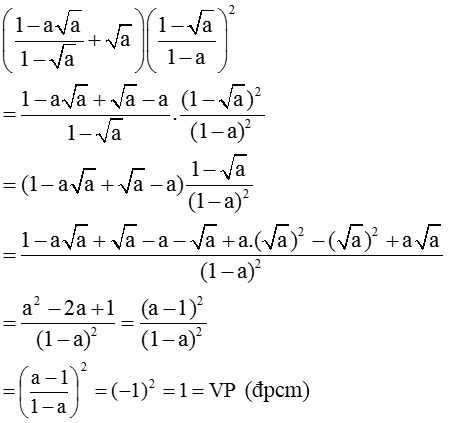
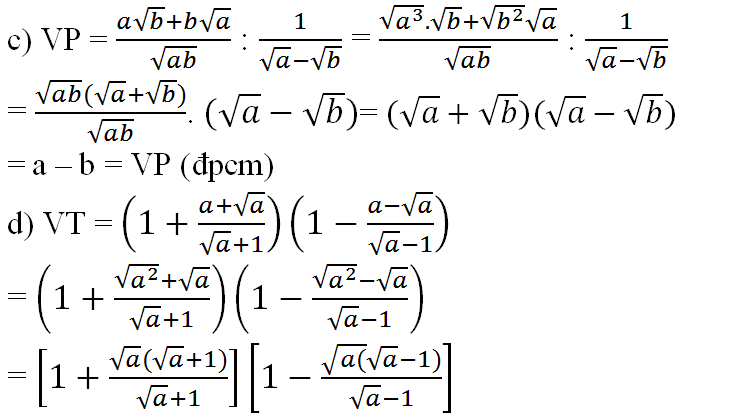
\(\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\cdot\left(\dfrac{1-\sqrt{a}}{1-a}\right)^2\)
\(=\left(\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}+\sqrt{a}\right)\cdot\left(\dfrac{1-\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}\right)^2\)
\(=\left(1+\sqrt{a}+a+\sqrt{a}\right)\cdot\left(\dfrac{1}{1+\sqrt{a}}\right)^2\)
\(=\dfrac{\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}+1\right)^2}=1\)