17. Cho hv ABCD, trên cạnh BC lấy M ( BM<MC). Từ A kẻ Ax⊥AM cắt CD tại N
a, cm AN=AM
b, Bd cắt MN tại Q. AQ cắt DC tại K. CM DK/DC=DQ/QB
c, Lấy điểm P∈BD sao cho PM⊥BC. CM NDMP là hbh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM vuông tại B và ΔBCN vuông tại C có
AB=BC
BM=CN
=>ΔABM=ΔBCN
=>AM=BN
b: ΔABM=ΔBCN
=>góc BMA=góc CNB
mà góc CNB+góc CBN=90 độ
nên góc BMA+góc CBN=90 độ
=>AM vuông góc BN

Kí hiệu diện tích là S
Vì : \(BM=\frac{1}{2}BC\Rightarrow BM=18\times\frac{1}{2}=9\left(cm\right)\)
\(CN=\frac{1}{3}CD\Rightarrow CN=24\times\frac{1}{3}=8\left(cm\right)\)
Cạnh DN dài là : 24 - 8 = 16 ( cm )
SABM là : 24 x 9 : 2 = 108 ( cm2 )
SMCN là : 9 x 8 : 2 = 36 ( cm2 )
SADN là : 18 x 16 : 2 = 164 ( cm2 )
SABCD là : 24 x 18 = 432 ( cm2 )
Vậy SAMN là : ... ( tự lm )

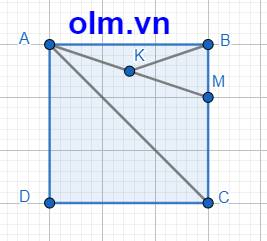
SABCD = 12 \(\times\)12 = 144 (cm2)
SABC = 12 \(\times\) 12 : 2 = 72 (cm2)
BM = 12 \(\times\) \(\dfrac{2}{3}\) = 8 (cm)
CM = 12 - 8 = 4 (cm)
SACM = 12 \(\times\)4 : 2 = 24 (cm2)
b, SABK = \(\dfrac{1}{2}\)SABM (vì hai tam giác có chung đường cao hạ từ đỉnh B xuống đáy BM và AK = \(\dfrac{1}{2}\)AM)
SABM = SABC - SAMC = 72 - 24 = 48 (cm2)
SABK = 48 : 2 = 24 (cm2)
Đáp số: a, SABCD = 144 cm2; SACM = 24 cm2
b, SABK = 24 cm2
a: Ta có: \(\widehat{BAM}+\widehat{DAM}=\widehat{BAD}=90^0\)
\(\widehat{MAD}+\widehat{NAD}=\widehat{MAN}=90^0\)
Do đó: \(\widehat{BAM}=\widehat{NAD}\)
Xét ΔABM vuông tại B và ΔADN vuông tại D có
AB=AD
\(\widehat{BAM}=\widehat{DAN}\)
Do đó: ΔABM=ΔADN
=>AM=AN