Tìm x
12 x -33=3^2 . 3^3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 12 2021
\(a,12\left(x-1\right)=0\\ x-1=0\\ x=1\\ b,45+5\left(x-3\right)=70\\ 5\left(x-3\right)=25\\ x-3=5\\ x=8\\ c,3.x-18:2=12\\ 3.x-9=12\\ 3.x=21\\ x=7\)
CL
1
4 tháng 6 2023
Ta nhận thấy tổng các hệ số trong phương trình đã cho là
\(1-2\left(m-1\right)+2m-3=0\) nên pt này luôn có 1 nghiệm bằng 1, còn nghiệm kia là \(2m-3\). Do vai trò của \(x_1,x_2\) trong \(x^2+2x_1x_2-x_2=1\) là không như nhau nên ta phải chia làm 2TH:
TH1: \(x_1=1;x_2=2m-3\). Khi đó ta có
\(1+2\left(2m-3\right)-\left(2m-3\right)=1\) \(\Leftrightarrow2m-3=0\) \(\Leftrightarrow m=\dfrac{3}{2}\)
TH2: \(x_1=2m-3;x2=1\). Khi đó
\(\left(2m-3\right)^2+2\left(2m-3\right)-1=1\) \(\Leftrightarrow4m^2-8m+1=0\) \(\Leftrightarrow m=\dfrac{2\pm\sqrt{3}}{2}\)
Vậy để pt đã cho có 2 nghiệm \(x_1,x_2\) thỏa ycbt thì \(\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=\dfrac{2\pm\sqrt{3}}{2}\end{matrix}\right.\)
LN
1
27 tháng 1 2023
Ta thấy các hệ số \(a,b,c\) của phương trình đã cho thỏa mãn \(a-b+c=1-\left[-\left(m-3\right)\right]-m+2=1+m-3-m+2=0\)
nên phương trình đã cho sẽ có một nghiệm là \(-1\) và nghiệm kia là \(m-2\).
Trong hệ thức \(x_1^2+x_2=8\), vai trò của \(x_1,x_2\) không như nhau nên ta xét 2 trường hợp:
TH1: Nếu \(x_1=-1\) thì \(x_1^2+x_2=8\Leftrightarrow\left(-1\right)^2+m-2=8\Leftrightarrow m=9\).
TH2: Nếu \(x_2=-1\) thì \(x_1^2+x_2=8\Leftrightarrow\left(m-2\right)^2-1=8\Leftrightarrow\left(m-2\right)^2=9\) \(\Leftrightarrow m-2=\pm3\) \(\Leftrightarrow\left[{}\begin{matrix}m=5\\m=-1\end{matrix}\right.\).
Vậy để phương trình đã cho có 2 nghiệm thỏa điều kiện đề cho thì \(\left[{}\begin{matrix}m=-1\\m=5\\m=9\end{matrix}\right.\)
LN
1
AH
Akai Haruma
Giáo viên
28 tháng 1 2023
Lời giải:
Để pt có 2 nghiệm thì $\Delta=(m-3)^2-4(-m+2)\geq 0$
$\Leftrightarrow (m-1)^2\geq 0$ (luôn đúng với mọi $m\in\mathbb{R}$)
Áp dụng định lý Viet:
$x_1+x_2=m-3$
$x_1x_2=-m+2$
$\Rightarrow x_1+x_2+x_1x_2=-1$
$\Leftrightarrow x_1+x_2+x_1x_2+1=0$
$\Leftrightarrow (x_1+1)(x_2+1)=0$
$\Leftrightarrow x_1=-1$ hoặc $x_2=-1$
TH1: $x_1=-1$
$x_2=\frac{-m+2}{x_1}=m-2$. Khi đó:
$x_1^2+x_2=8$
$\Leftrightarrow (-1)^2+(m-2)=8$
$\Leftrightarrow m=9$
TH2: $x_2=-1$
$x_1=\frac{-m+2}{x_2}=m-2$. Khi đó:
$x_1^2+x_2=8$
$\Leftrightarrow (m-2)^2-1=8$
$\Leftrightarrow (m-2)^2=9$
$\Leftrightarrow m-2=\pm 3\Leftrightarrow m=5$ hoặc $m=-1$
12 tháng 4 2021
Trước hết ta xét ĐK của m để pt có hai nghiệm phân biệt
Ta có : Δ = b2 - 4ac = ( 2m - 3 )2 - 4( -2m + 2 )
= 4m2 - 12m + 9 + 8m - 8
= 4m2 - 4m + 1 = ( 2m - 1 )2 > 0 ∀ m ≠ 1/2
Vậy ∀ m ≠ 1/2 thì pt có hai nghiệm phân biệt
Theo hệ thức Viète ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-2m+3\\x_1x_2=\dfrac{c}{a}=-2m+2\end{matrix}\right.\)
Khi đó x12 + x22 = 17
<=> ( x1 + x2 )2 - 2x1x2 - 17 = 0
<=> ( -2m + 3 )2 - 2( -2m + 2 ) - 17 = 0
<=> 4m2 - 12m + 9 + 4m - 4 - 17 = 0
<=> 4m2 - 8m - 12 = 0
<=> m2 - 2m - 3 = 0
<=> ( m - 3 )( m + 1 ) = 0
<=> m = 3 hoặc m = -1 (tm)
=> Chọn A.2
PT
1
CM
12 tháng 6 2018
c) Theo định lí Vi-et ta có:
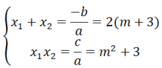
P = x 1 2 + x 2 2 = (x1 + x2 )2 - 2 x 1 x 2 = 4 m + 3 2 - 2( m 2 + 3)
= 4( m 2 + 6m + 9) - 2( m 2 + 3) = 2 m 2 + 24m + 30
PT
3
VV
10 tháng 8 2021
\(2^3x+5^2x=2.\left(5^2+2^3\right)-33\)
\(8x+25x=2.\left(25+8\right)-33\)
\(8x+25x=2.33-33\)
\(8x+25x=66-33\)
\(8x+25x=33\)
\(x+\left(8+25\right)=33\)
\(x+33=33\)
\(x=0\)
VV
10 tháng 8 2021
\(15:\left(x+2\right)=\left(3^3+3\right):10\)
\(15:\left(x+2\right)=\left(27+3\right):10\)
\(15:\left(x+2\right)=30:10\)
\(15:\left(x+2\right)=3\)
\(x+2=15:3\)
\(x+2=5\)
\(x=3\)
=>12x-33=3^5
=>12x=276
=>x=23
12x-33=9.27
12x-33=243
12x=243+33
12x=276
x=276:12
x=23