Giúp em bài này ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Cách làm ngắn gọn: \(5=\dfrac{5\left(x-1\right)}{x-1}=\dfrac{5x-5}{x-1}=\dfrac{5x+5-10}{x-1}\)
Do đó chọn \(f\left(x\right)=5x+5\) thế vào nhanh chóng tính ra kết quả giới hạn
Còn cách khác phức tạp hơn (có thể sử dụng cho tự luận):
Do \(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}=5\) hữu hạn nên \(f\left(x\right)-10=0\) có nghiệm \(x=1\)
\(\Rightarrow f\left(1\right)-10=0\Rightarrow f\left(1\right)=10\)
Do đó:
\(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{\left(\sqrt{x}-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}=\lim\limits_{x\rightarrow1}\dfrac{\left[f\left(x\right)-10\right]\left(\sqrt{x}+1\right)}{\left(x-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}.\dfrac{\sqrt{x}+1}{\sqrt{4f\left(x\right)+9}+3}=5.\dfrac{1+1}{\sqrt{4f\left(1\right)+9}+3}=5.\dfrac{2}{\sqrt{4.10+9}+3}=...\)



\(n_{Br_2}=\dfrac{8}{160}=0,05\left(mol\right)\)
PTHH: C2H4 + Br2 --> C2H4Br2
0,05<--0,05
=> \(\%V_{C_2H_4}=\dfrac{0,05.22,4}{4,48}.100\%=25\%\)
\(\%V_{CH_4}=100\%-25\%=75\%\)

Câu 2:
a: Không
b: Không
Câu 3:
a: \(\widehat{B}=\widehat{zAB}\left(=124^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên Bt//Az
b: n\(\perp\)DC
m\(\perp\)DC
Do đó: n//m
c: \(\widehat{xEG}+\widehat{yGE}=70^0+110^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên Ex//Gy
d: Vẽ lại hình, ta sẽ có:
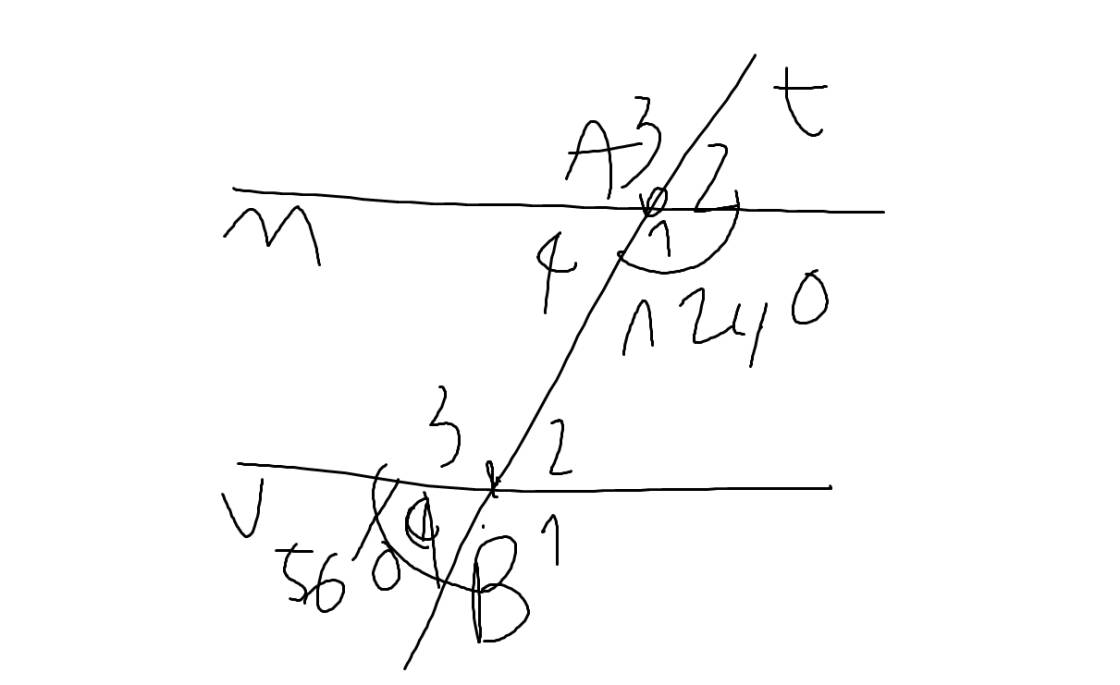
Ta có: \(\widehat{B_4}=\widehat{B_2}\)(hai góc đối đỉnh)
mà \(\widehat{B_4}=56^0\)
nên \(\widehat{B_2}=56^0\)
Ta có: \(\widehat{A_1}+\widehat{B_2}=124^0+56^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên m//v


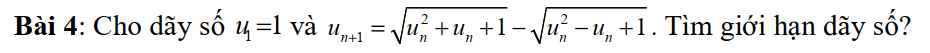




 may bai nay kho qua giup em , em dang can gap a
may bai nay kho qua giup em , em dang can gap a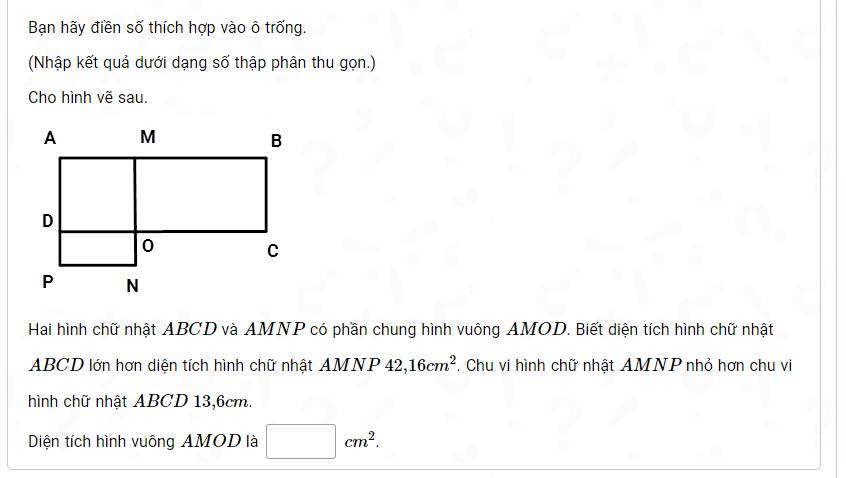
a: \(G\in\left(SAD\right)\)
\(G\in GB\subset\left(GBC\right)\)
Do đó: \(G\in\left(SAD\right)\cap\left(GBC\right)\)
Xét (SAD) và (GBC) có
\(G\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó:(SAD) giao (SBC)=xy,xy đi qua G và xy//AD//BC
b: ABCD là hình bình hành tâm O
nên O là trung điểm chung của AC và BD
Xét ΔACB có
I,O lần lượt là trung điểm của CB,CA
=>IO là đường trung bình của ΔCAB
=>IO//AB
IO//AB
AB\(\subset\)(SAB)
IO không thuộc mp(SAB)
Do đó: IO//(SAB)
c: Xét ΔSAC có
H,O lần lượt là trung điểm của CS,CA
=>HO là đường trung bình của ΔSAC
=>HO//SA
HO//SA
SA\(\subset\)(SAB)
HO không nằm trong mp(SAB)
Do đó: HO//(SAB)
Ta có: IO//(SAB)
HO//(SAB)
IO,HO\(\subset\)(OHI)
Do đó: (OHI)//(SAB)