cho tam giác ABC có goc A=100o , góc B - C = 50o.Tính góc B,C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 8 2017
Ta có ∠A + ∠(ABC) + ∠(ACB) = 180o ⇒ ∠(ABC) + ∠(ACB) = 80o
Có ∠(ABO) + ∠(OBC) + ∠(BCO) + ∠(OCA) = 2.∠(OBC) + 2.∠(BCO) = 2(∠(OBC) + ∠(BCO)) = 80o
⇒ ∠(OBC) + ∠(BCO) = 40o ⇒ (BOC) = 140o. Ta có ∠A + ∠(ABC) + ∠(ACB) = 180o ⇒ ∠(ABC) + ∠(ACB) = 80o
Có ∠(ABO) + ∠(OBC) + ∠(BCO) + ∠(OCA) = 2.∠(OBC) + 2.∠(BCO) = 2(∠(OBC) + ∠(BCO)) = 80o
⇒ ∠(OBC) + ∠(BCO) = 40o ⇒ (BOC) = 140o. Chọn C
DH
0
PT
1
CM
8 tháng 11 2019
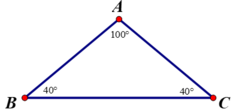
Tam giác ABC là tam giác tù vì có 1 góc A tù.
Áp dụng định lý tổng ba góc trong tam giác ABC ta có:
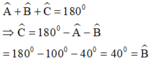
Suy ra ∆ABC cân tại A.
PT
1
CM
17 tháng 9 2018
Trong tam giác ABC có góc A là góc tù nên cạnh đối diện với góc A là cạnh lớn nhất.
Cạnh đối diện với góc A là BC nên suy ra cạnh BC lớn nhất.
CM
2 tháng 7 2017
Ta có ∠C = 180o - 30o - 100o = 50o
Khi đó ∠(ACE) = 50o : 2 = 25o. Chọn D
CM
19 tháng 5 2017
Ta có ∠C = 180o - 30o - 100o = 50o
Khi đó ∠(ACE) = 50o : 2 = 25o. Chọn D
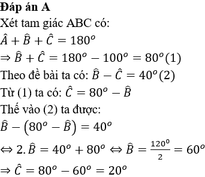
^B+^C=1800-1000=800
=> ^C=(800-500)/2=150
^B=150+500=650
ĐS: ^B=650; ^C=150.
Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) và \(\widehat{A}=100^o\) ; \(\widehat{B}-\widehat{C}=50^o\)
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}-\widehat{A}=180^o-100^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=80^0\) mà \(\widehat{B}-\widehat{C}=50^0\)
\(\Rightarrow\widehat{B}=\left(\widehat{B}+\widehat{C}-\left(\widehat{B}-\widehat{C}\right)\right)\left(80^o+50^0\right):2=65^0\)
\(\Rightarrow\widehat{C}=\widehat{B}-50^0=65^0-50^0=15^0\)