Cho dãy số (Un) được xác định như sau: Un là số dư của số tự nhiên n trong phép chia cho 6
a) Tính 7 số hạng đầu tiên của dãy số
b) Chứng minh rằng: Nếu \(U_m=U_n\) thì \(\left|m-n\right|\) chia hết cho 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 12 2017
Chọn B.
Ta có: u1 = 1; u2 = 3/2; u3 = 17/6; u4 = 227/34.
Ta chứng minh un > 0 bằng quy nạp.
Giả sử un > 0, khi đó: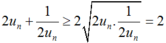 
Nên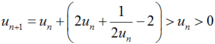 
.
M
30 tháng 8 2023
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:
u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15
Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:
n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10
Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = (2n - 1)/(n + 1):u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5
Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:
(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1
Vậy số hạng thứ mấy có giá trị 137137 là u1.
27 tháng 11 2023
Đặt \(\dfrac{u_n}{n+1}=v_n\)
\(GT\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{u_1}{1+1}=1\\v_{n+1}=\dfrac{1}{4}v_n,\forall n\in N\text{*}\end{matrix}\right.\)
\(\Rightarrow v_n=\dfrac{1}{4}^{n-1},\forall n\in N\text{*}\)
\(\Rightarrow u_n=\left(n+1\right).\dfrac{1}{4}^{n-1},\forall n\in N\text{*}\)
a: \(u_1=1;u_2=2;u_3=3;u_4=4;u_5=5;u_6=0;u_7=1\)
b: m=6k+a;n=6c+d
\(u_m=u_n\)
=>a=d
=>\(m=6k+a;n=6c+a\)
\(\left|m-n\right|=\left|6k+a-6c-a\right|=\left|6k-6c\right|=6\left|k-c\right|⋮6\)