Cho hàm số y=(m2+m-2)x+3m2-m-1(1).Xác định m để:
a) Hàm số (1) là bậc nhất.Khi đó tìm m để hàm số đó nghịch biến
b) Hàm số m là hàm hằng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
24 tháng 9 2023
a) \(y=\left(m+2\sqrt{m}+1\right)x-10\) là hàm số đồng biến khi: \(\left(m\ge0\right)\)
\(m+2\sqrt{m}+1>0\)
\(\Leftrightarrow\left(\sqrt{m}+1\right)^2>0\) (luôn đúng)
Nên hàm số này luôn là hàm số đồng biến với \(m\ge3\)
b) \(y=\left(\sqrt{m}-3\right)x+2\) là hàm số nghịch biến khi: \(\left(m\ge0\right)\)
\(\sqrt{m}-3< 0\)
\(\Leftrightarrow\sqrt{m}< 3\)
\(\Leftrightarrow m< 9\)
\(\Leftrightarrow0\le m< 9\)
S
2 tháng 9 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
15 tháng 8 2023
1:
a: m^2+1>=1>0 với mọi m
=>y=(m^2+1)x-5 luôn là hàm số bậc nhất
b: Do m^2+1>0 với mọi m
nên hàm số y=(m^2+1)x-5 đồng biến trên R
24 tháng 10 2021
a) Hàm số đồng biến trên R\(\Rightarrow a>0\Rightarrow m-2>0\Rightarrow m>2\)
b) Hàm số nghịch biến trên R
\(\Leftrightarrow a< 0\Rightarrow m-2< 0\Rightarrow m< 2\)
IL
19 tháng 7 2021
a) Để hàm số đã cho là hàm bậc nhất thì
b) Để hàm số đã cho đồng biến trên tập xác định thì :
c) Để hàm số đã cho nghịch biến trên tập xác định thì:
19 tháng 7 2021
a) Để hàm số là hàm số bậc nhất thì \(2-m\ne0\)
\(\Leftrightarrow m\ne2\)
b) Để hàm số đồng biến thì 2-m>0
hay m<2
c) Để hàm số nghịch biến thì 2-m<0
hay m>2
30 tháng 1 2023
a: Để (1) đồng biến thì m-1>0
=>m>1
Để (1) nghịch biến thì m-1<0
=>m<1
b: Khi m=0 thì (1) sẽ là y=-x+2
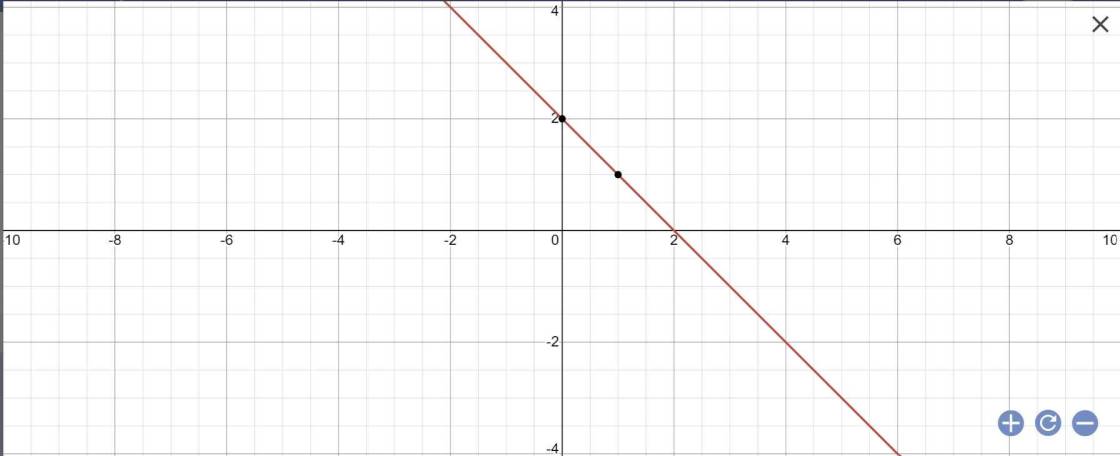c: y=(m-1)x+2-m
=mx-x+2-m
=m(x-1)-x+2
Điểm mà (1) luôn đi qua là:
x-1=0 và y=-x+2
=>x=1 và y=-1+2=1
13 tháng 1 2023
a: Để hàm số đồng biến thì m+1>0
=>m>-1
Để hàm số nghịch biến thì m+1<0
=>m<-1
b: Để hai đường song song thì m+1=2
=>m=1
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
15 tháng 10 2023
\(Ta.có:y=ax+b\)
HSĐB khi a>0 ; HSNB khi a<0
Từ đây em giải các a ra thôi nè!
15 tháng 10 2023
a: Để hàm số đồng biến thì 2m-10>0
=>2m>10
=>m>5
b: Để hàm số đồng biến thì 2-5m>0
=>5m<2
=>m<2/5
c: Để hàm số nghịch biến thì 3-7m<0
=>7m>3
=>m>3/7
d:
\(y=m\left(3-2x\right)+x-2\)
\(=3m-2mx+x-2\)
\(=x\left(-2m+1\right)+3m-2\)
Để hàm số nghịch biến thì -2m+1<0
=>-2m<-1
=>m>1/2
e: Để đây là hàm số bậc nhất thì \(\left\{{}\begin{matrix}m>=0\\3-\sqrt{m}\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>=0\\m\ne9\end{matrix}\right.\)
f: Để đây là hàm số bậc nhất thì
\(\left\{{}\begin{matrix}m-2>=0\\\sqrt{m-2}-1< >0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>=2\\\sqrt{m-2}< >1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>=2\\m-2< >1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>=2\\m< >3\end{matrix}\right.\)
g: Để hàm số đồng biến thì \(m^2+6m+9>0\)
=>\(\left(m+3\right)^2>0\)
=>m+3<>0
=>m<>-3
h: Để đây là hàm số bậc nhất thì \(\dfrac{m-1}{m-4}\ne0\)
=>\(m\notin\left\{1;4\right\}\)
a: Để hàm số (1) là hàm số bậc nhất thì \(m^2+m-2< >0\)
=>\(m^2+2m-m-2< >0\)
=>\(\left(m+2\right)\left(m-1\right)< >0\)
=>\(\left\{{}\begin{matrix}m+2< >0\\m-1< >0\end{matrix}\right.\Leftrightarrow m\notin\left\{-2;1\right\}\)
Để hàm số nghịch biến thì (m+2)(m-1)<0
TH1: \(\left\{{}\begin{matrix}m+2>0\\m-1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>-2\\m< 1\end{matrix}\right.\)
=>-2<m<1
TH2: \(\left\{{}\begin{matrix}m+2< 0\\m-1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>1\\m< -2\end{matrix}\right.\)
=>Loại
b: Để hàm số (1) là hàm hằng thì \(m^2+m-2=0\)
=>(m+2)(m-1)=0
=>\(\left[{}\begin{matrix}m+2=0\\m-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=-2\end{matrix}\right.\)