Cho x + y = 1
Tìm giá trị nhỏ nhất của M = 3x2 + y2 + 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 8 2023
Tìm giá trị nhỏ nhất của biểu thức:
a) Ta có:
\(M=2x^2+4x+7\)
\(M=2\cdot\left(x^2+2x+\dfrac{7}{2}\right)\)
\(M=2\cdot\left(x^2+2x+1+\dfrac{5}{2}\right)\)
\(M=2\cdot\left[\left(x+1\right)^2+2,5\right]\)
\(M=2\left(x+1\right)^2+5\)
Mà: \(2\left(x+1\right)^2\ge0\forall x\) nên:
\(M=2\left(x+1\right)^2+5\ge5\forall x\)
Dấu "=" xảy ra:
\(2\left(x+1\right)^2+5=5\Leftrightarrow2\left(x+1\right)^2=0\)
\(\Leftrightarrow\left(x+1\right)^2=0\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
Vậy: \(M_{min}=5\) khi \(x=-1\)
b) Ta có:
\(N=x^2-x+1\)
\(N=x^2-2\cdot\dfrac{1}{2}\cdot x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(N=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Mà: \(\left(x+\dfrac{1}{2}\right)^2\ge0\forall x\) nên \(N=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=" xảy ra:
\(\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=\dfrac{3}{4}\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2=0\)
\(\Leftrightarrow x-\dfrac{1}{2}=0\Leftrightarrow x=\dfrac{1}{2}\)
Vậy: \(N_{min}=\dfrac{3}{4}\) khi \(x=\dfrac{1}{2}\)
19 tháng 8 2023
Tìm giá trị lớn nhất của biểu thức
a) Ta có:
\(E=-4x^2+x-1\)
\(E=-\left(4x^2-x+1\right)\)
\(E=-\left[\left(2x\right)^2-2\cdot2x\cdot\dfrac{1}{4}+\dfrac{1}{16}+\dfrac{15}{16}\right]\)
\(E=-\left[\left(2x-\dfrac{1}{4}\right)^2+\dfrac{15}{16}\right]\)
Mà: \(\left(2x+\dfrac{1}{4}\right)^2+\dfrac{15}{16}\ge\dfrac{15}{16}\forall x\) nên
\(\Rightarrow E=-\left[\left(2x+\dfrac{1}{4}\right)^2+\dfrac{15}{16}\right]\le-\dfrac{15}{16}\forall x\)
Dấu "=" xảy ra:
\(-\left[\left(2x+\dfrac{1}{4}\right)^2+\dfrac{15}{16}\right]=-\dfrac{15}{16}\Leftrightarrow-\left(2x+\dfrac{1}{4}\right)^2-\dfrac{15}{16}=-\dfrac{15}{16}\)
\(\Leftrightarrow-\left(2x+\dfrac{1}{4}\right)^2=0\Leftrightarrow2x-\dfrac{1}{4}=0\Leftrightarrow x=\dfrac{1}{16}\)
Vậy: \(E_{max}=-\dfrac{15}{16}\) khi \(x=\dfrac{1}{16}\)
b) Ta có:
\(F=5x-3x^2+6\)
\(F=-3x^2+5x-6\)
\(F=-\left(3x^2-5x-6\right)\)
\(F=-3\left(x^2-\dfrac{5}{3}x-2\right)\)
\(F=-3\left[\left(x-\dfrac{5}{6}\right)^2-\dfrac{97}{36}\right]\)
\(F=-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{97}{36}\)
Mà: \(-3\left(x-\dfrac{5}{6}\right)^2\le0\forall x\) nên:
\(F=-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{97}{36}\le\dfrac{97}{36}\forall x\)
Dấu "=" xảy ra:
\(-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{97}{36}=\dfrac{97}{36}\Leftrightarrow-3\left(x-\dfrac{5}{6}\right)^2=0\)
\(\Leftrightarrow x-\dfrac{5}{6}=0\Leftrightarrow x=\dfrac{5}{6}\)
Vậy: \(F_{max}=\dfrac{97}{36}\) khi \(x=\dfrac{5}{6}\)
AH
Akai Haruma
Giáo viên
13 tháng 8 2021
Bài 1:
Ta thấy: $(x+\frac{1}{2})^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow (x+\frac{1}{2})^2+\frac{5}{4}\geq \frac{5}{4}$
Vậy gtnn của biểu thức là $\frac{5}{4}$
Giá trị này đạt tại $x+\frac{1}{2}=0\Leftrightarrow x=-\frac{1}{2}$
AH
Akai Haruma
Giáo viên
13 tháng 8 2021
Bài 2:
$x+y-3=0\Rightarrow x+y=3$
\(M=x^2(x+y)-(x+y)x^2-y(x+y)+4y+x+2019\)
\(=-3y+4y+x+2019=x+y+2019=3+2019=2022\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 11 2021
Chắc đề đúng là số dương, vì ko tồn tại x;y nguyên dương thỏa mãn x+y=1
\(A=\dfrac{y^2}{xy+y}+\dfrac{x^2}{xy+x}\ge\dfrac{\left(x+y\right)^2}{x+y+2xy}\ge\dfrac{\left(x+y\right)^2}{x+y+\dfrac{1}{2}\left(x+y\right)^2}=\dfrac{2}{3}\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)
17 tháng 12 2023
Bài 1:
a: \(M=x^2-10x+3\)
\(=x^2-10x+25-22\)
\(=\left(x^2-10x+25\right)-22\)
\(=\left(x-5\right)^2-22>=-22\forall x\)
Dấu '=' xảy ra khi x-5=0
=>x=5
b: \(N=x^2-x+2\)
\(=x^2-x+\dfrac{1}{4}+\dfrac{7}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>=\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x-1/2=0
=>x=1/2
c: \(P=3x^2-12x\)
\(=3\left(x^2-4x\right)\)
\(=3\left(x^2-4x+4-4\right)\)
\(=3\left(x-2\right)^2-12>=-12\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2
T
15 tháng 10 2023
\(a,A=x^2+y^2\\=x^2-2xy+y^2+2xy\\=(x-y)^2+2xy\\=2^2+2\cdot1\\=4+2\\=6\)
\(b,x+y=1\\\Leftrightarrow (x+y)^3=1^3\\\Leftrightarrow x^3+3x^2y+3xy^2+y^3=1\\\Leftrightarrow x^3+3xy(x+y)+y^3=1\\\Leftrightarrow x^3+3xy\cdot1+y^3=1\\\Rightarrow A=1\)
15 tháng 10 2023
a) Ta có:
\(x-y=2\)
\(\Rightarrow\left(x-y\right)^2=2^2\)
\(\Rightarrow x^2-2xy+y^2=4\)
Mà: \(xy=1\)
\(\Rightarrow\left(x^2+y^2\right)-2\cdot1=4\)
\(\Rightarrow x^2+y^2=4+2\)
\(\Rightarrow x^2+y^2=6\)
b) Ta có:
\(x+y=1\)
\(\Rightarrow\left(x+y\right)^3=1^3\)
\(\Rightarrow x^3+3x^2y+3xy+y^3=1\)
\(\Rightarrow x^3+3xy\left(x+y\right)+y^3=1\)
Mà: x + y = 1
\(\Rightarrow x^3+3xy\cdot1+y^3=1\)
\(\Rightarrow x^3+3xy+y^3=1\)
CM
11 tháng 11 2019
Đáp án B
Ta có:
3 x 2 + y 2 − 2 . log 2 x − y = 1 2 1 + log 2 1 − x y ⇔ 3 x 2 + y 2 − 2 . log 2 x − y 2 = log 2 2 − 2 x y
⇔ 3 x 2 + 2 x y + y 2 − 2 + 2 x y . log 2 x − y 2 = log 2 2 − 2 x y ⇔ 3 x − y 2 . log 2 x − y = 3 2 − 2 x y . log 2 2 − 2 x y
Xét hàm số f t = 3 t . log 2 t trên khoảng 0 ; + ∞ , có f ' t = 3 t ln 3. log 2 t + 3 t t . ln 2 > 0 ; ∀ t > 0
Suy ra f t là hàm số đồng biến trên 0 ; + ∞ mà
f x − y 2 = f 2 − 2 x y ⇒ x 2 + y 2 = 2
Khi đó:
M = 2 x 3 + y 3 − 3 x y = 2 x + y x + y 2 − 3 x y − 3 x y ⇔ 2 M = 2 x + y 2 x + y 2 − 3.2 x y − 3.2 x y 2 x + y 2 x + y 2 − 3 x + y 2 + 6 − 3 x + y 2 + 6 = 2 x + y 6 − x + y 2 − 3 x + y 2 + 6 = − 2 a 3 − 3 a 2 + 12 a + 6 ,
Với a = x + y ∈ 0 ; 4
Xét hàm số f a = − 2 a 3 − 3 a 2 + 12 a + 6 trên 0 ; 4 ,
suy ra m ax 0 ; 4 f a = 13.
Vậy giá trị lớn nhất của biểu thức M là 13 2
CM
10 tháng 6 2017
Đáp án B
Ta có
3 x 2 + y 2 − 2 . log 2 x − y = 1 2 1 + log 2 1 − x y ⇔ 3 x 2 + y 2 − 2 . log 2 x − y 2 = log 2 2 − 2 x y
⇔ 3 x 2 + 2 x y + y 2 − 2 + 2 x y . log 2 x − y 2 = log 2 2 − 2 x y ⇔ 3 x − y 2 . log 2 x − y = 3 2 − 2 x y . log 2 2 − 2 x y
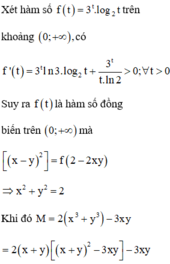
⇔ 2 M = 2 x + y 2 x + y 2 − 3.2. x y − 3.2 x y = 2 x + y 2 x + y 2 − 3 x + y 2 + 6 − 3 x + y 2 + 6
= 2 x + y 6 − x + y 2 − 3 x + y 2 + 6 = − 2 a 3 − 3 a 2 + 12 a + 6 ,
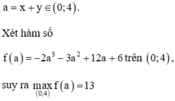
Vậy giá trị lớn nhất của biểu thức M là 13 2
Ta có \(x+y=1\Rightarrow y=1-x\)
\(\Rightarrow M=3x^2+y^2+2=3x^2+\left(1-x\right)^2+2=3x^2+x^2-2x+1+2\)
\(=4x^2-2x+3=\left[\left(2x\right)^2-2.2x.\frac{1}{2}+\frac{1}{4}\right]+\frac{11}{4}\)
\(=\left(2x-\frac{1}{2}\right)^2+\frac{11}{4}\ge\frac{11}{4}\forall x\) có GTNN là \(\frac{11}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}2x-\frac{1}{2}=0\\x+y=1\end{cases}\Rightarrow\hept{\begin{cases}x=\frac{1}{4}\\y=\frac{3}{4}\end{cases}}}\)
Vậy \(M_{min}=\frac{11}{4}\) tại \(x=\frac{1}{4};y=\frac{3}{4}\)
x+y=1 => x=0 , y=1 hoac x=1 va y=0
khi x=0 va y=1 thi : M = 3 x 02 + 12 + 2=3
khi x=1 va y=0 thi : M = 3 x 12 + 02+ 2 =5
vậy giá trị nhỏ nhất của M là 3