Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Tiếp tuyến tại \(A\) với đường tròn ngoại tiếp tam giác \(ABC\) cắt các tiếp tuyến tại \(B\) và \(C\) lần lượt của \(D\) và \(E\). Gọi \(I\) là giao điểm \(CD\) và \(BE\). Chứng minh rằng:
\(a\)) \(A,I,H\) thẳng hàng.
\(b\)) \(AI=IH\).
\(c\)) \(DE\cdot AI=DB\cdot EC\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

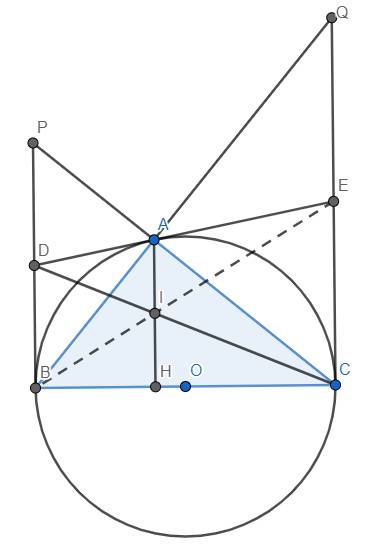
a) và b) Gọi \(P=CA\cap BD,Q=BA\cap CE\)
Tam giác ABP vuông tại A \(\Rightarrow\widehat{DAP}=90^o-\widehat{DAB}\) và \(\widehat{P}=90^o-\widehat{DBA}\)
Dễ thấy tam giác DAB cân tại D nên \(\widehat{DAB}=\widehat{DBA}\). Từ đó suy ra \(\widehat{DAP}=\widehat{P}\) hay tam giác DAP cân tại D \(\Rightarrow DA=DB=DP\) hay D là trung điểm BP. Tương tự, ta có E là trung điểm CQ.
Gọi \(I'=CD\cap AH\). Khi đó áp dụng bổ đề hình thang cho hình thang AHBP, ta có ngay I' là trung điểm AH. Lại áp dụng bổ đề hình thang lần nữa cho hình thang AHCQ, ta thấy B, I, E thẳng hàng (*)
(*) Bổ đề hình thang phát biểu rằng: Trong 1 hình thang, 2 trung điểm của 2 cạnh đáy, giao điểm 2 đường chéo và giao điểm của 2 đường thẳng chứa 2 cạnh bên của nó thẳng hàng.
Do đó \(I'\equiv I\), suy ra I, A, H thẳng hàng, đồng thời \(IA=IH\).
c) Theo Thales: \(\dfrac{DA}{DE}=\dfrac{AI}{EC}\) \(\Rightarrow DE.AI=DA.EC\). Mà \(DA=DB\) (tính chất 2 tiếp tuyến cắt nhau) nên ta có đpcm.
Thanks anh/chị Lê Song Phương nhiều ạ, nhờ có chị mà em hiểu rõ hơn về toán lớp 9 r ạ!#

Gọi M là trung điểm DE. Khi đó MO là đường TB của hình thang BCED => MO vg với BC
Mà M là tâm đường tròn đường kính DE => DE là tiếp tuyến ...

a) Ta có: \(\left\{{}\begin{matrix}BD=AD\\CE=AE\end{matrix}\right.\)(t/c 2 tiếp tuyến cắt nhau)
\(\Rightarrow BD+CE=AD+AE=ED\)
b) Ta có: \(\left\{{}\begin{matrix}\widehat{AOD}=\widehat{BOD}=\dfrac{1}{2}\widehat{AOB}\\\widehat{AOE}=\widehat{EOC}=\dfrac{1}{2}\widehat{AOC}\end{matrix}\right.\)(t/c 2 tiếp tuyến cắt nhau)
\(\Rightarrow\widehat{DOE}=\widehat{AOD}+\widehat{AOE}=\dfrac{1}{2}\left(\widehat{AOB}+\widehat{AOC}\right)=\dfrac{1}{2}.180^0=90^0\)
(Do \(\widehat{AOB},\widehat{AOC}\) là 2 góc kề bù)
c) Gọi K là trung điểm DE
Ta có: \(DB\perp BC,EC\perp BC\Rightarrow BD//EC\)
\(\Rightarrow BDEC\) là hình thang
Ta có: Tam giác ABC vuông tại A nội tiếp đường tròn (O)
=> O là trung điểm cạnh huyền BC
Xét hthang BDEC có:
O là trung điểm BC(cmt)
K là trung điểm DE(cách vẽ)
=> OK là đường trung bình
\(\Rightarrow\left\{{}\begin{matrix}OK//EC\\OK=\dfrac{1}{2}\left(BD+EC\right)\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}OK=\dfrac{1}{2}DE=DK\\OK\perp BC\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}O\in\left(K\right)\\OK\perp BC\end{matrix}\right.\) => BC là tiếp tuyến đường tròn (K)

a) Theo tính chất của 2 tiếp tuyến cắt nhau \(\left\{{}\begin{matrix}AD=BD\\AE=CE\end{matrix}\right.\)
\(\Rightarrow\dfrac{AD}{AE}=\dfrac{BD}{CE}=\dfrac{ID}{IC}\)
\(\Rightarrow\) AI//CE.
Mà \(CE\perp BC\) nên \(AI\perp BC\)
Lại có \(AH\perp BC\) \(\Rightarrow\) A, I, H thẳng hàng (đpcm)
b) Theo định lý Thales, ta có \(\dfrac{AI}{CE}=\dfrac{DA}{DE}\) và \(\dfrac{IH}{CE}=\dfrac{BH}{BC}\)
Mặt khác, \(\dfrac{DA}{DE}=\dfrac{BH}{BC}\) (đl Thales trong hình thang)
\(\Rightarrow\dfrac{AI}{CE}=\dfrac{IH}{CE}\) \(\Rightarrow AI=IH\) (đpcm)
c) Ta có \(\dfrac{DB}{DE}=\dfrac{DA}{DE}=\dfrac{AI}{CE}\) \(\Rightarrow DB.CE=DE.AI\) (đpcm)