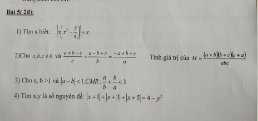giúp em bài 5 vs ạ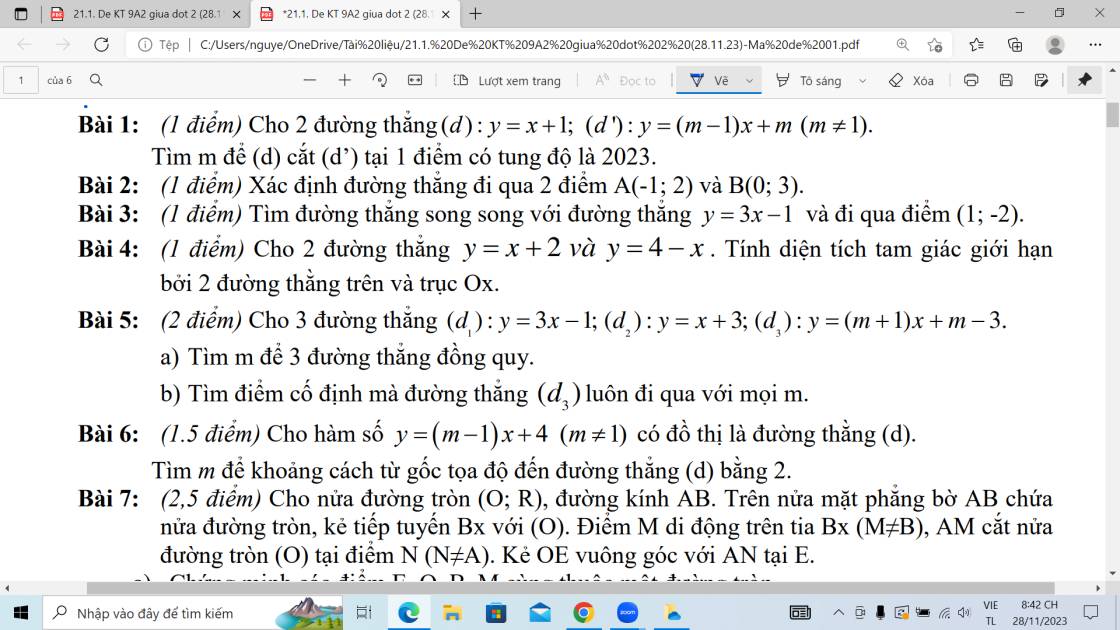
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 2:
1: \(\Leftrightarrow x\cdot\dfrac{7}{2}=\dfrac{9}{2}+3=\dfrac{15}{2}\)
hay x=15/7
2: \(\Leftrightarrow x=\dfrac{5}{2}\cdot\dfrac{8}{5}=4\)
3: \(\Leftrightarrow x=\dfrac{-11\cdot10}{5}=-11\cdot2=-22\)
4: =>2x=90
hay x=45


Bài 5:
a: TH1:m=0
=>x+1=0
=>x=-1(nhận)
TH2: m<>0
\(\text{Δ}=1^2-4m\left(m+1\right)=1-4m^2-4m\)
Để phương trình có nghiệm kép thì -4m^2-4m+1=0
=>\(m=\dfrac{-1\pm\sqrt{2}}{2}\)
b: Để phương trình có hai nghiệm phân biệt thì -4m^2-4m+1>=0
=>\(\dfrac{-1-\sqrt{2}}{2}< =m< =\dfrac{-1+\sqrt{2}}{2}\)
c: Để phương trình có hai nghiệm dương phân biệt thì
\(\left\{{}\begin{matrix}\dfrac{-1-\sqrt{2}}{2}< =m< =\dfrac{-1+\sqrt{2}}{2}\\\dfrac{-1}{m}>0\\\dfrac{m+1}{m}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-1-\sqrt{2}}{2}< =m< =\dfrac{-1+\sqrt{2}}{2}\\m< =-1\end{matrix}\right.\Leftrightarrow\dfrac{-1-\sqrt{2}}{2}< =m< =-1\)
d: Để phương trình có hai nghiệm trái dấu thì m(m+1)<0
=>-1<m<0
e: Để phương trình có hai nghiệm cùng dấu thì
\(\left\{{}\begin{matrix}\dfrac{-1-\sqrt{2}}{2}< =m< =\dfrac{-1+\sqrt{2}}{2}\\\dfrac{m+1}{m}>0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}0< m< =\dfrac{-1+\sqrt{2}}{2}\\\dfrac{-1-\sqrt{2}}{2}< =m< -1\end{matrix}\right.\)


5:
a: Xét ΔABC vuông tại A có
\(sinC=\dfrac{3}{5}\)
=>\(\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\dfrac{3}{BC}=\dfrac{3}{5}\)
=>BC=5(cm)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=5^2-3^2=16\)
=>AC=4(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\CH\cdot CB=CA^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AH=\dfrac{3\cdot4}{5}=2,4\left(cm\right)\\CH=\dfrac{4^2}{5}=3,2\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}\)
=>\(tanB=\dfrac{4}{3}\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
b: Xét ΔABF vuông tại A có AE là đường cao
nên \(BE\cdot BF=AB^2\left(1\right)\)
Xét ΔBAC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BE\cdot BF=BH\cdot BC\)
XétΔABC vuông tại A có AH là đường cao
nên \(CH\cdot CB=CA^2\)
\(\dfrac{AB^2}{AC^2}=\dfrac{BH\cdot BC}{CH\cdot CB}=\dfrac{BH}{CH}\)
c: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB
=>\(\widehat{MAB}=\widehat{MBA}\)
Xét ΔEAB vuông tại E và ΔHBA vuông tại H có
AB chung
\(\widehat{EAB}=\widehat{HBA}\)
Do đó: ΔEAB=ΔHBA
=>\(\widehat{DAB}=\widehat{DBA}\)
=>DA=DB
\(\widehat{DAB}+\widehat{DAF}=90^0\)
\(\widehat{DBA}+\widehat{DFA}=90^0\)
mà \(\widehat{DAB}=\widehat{DBA}\)
nên \(\widehat{DAF}=\widehat{DFA}\)
=>DA=DF
=>DF=DB
=>D là trung điểm của FB

Ta có ( x + 2 )( -x - 5 )( x2 + 9 ) = 0
Suy ra x + 2 = 0; -x - 5 = 0 hoặc x2 + 9 = 0
Nếu x + 2 = 0 ⇒ x = -2
Nếu -x - 5 = 0 ⇒ -x = 5 ( loại )
Nếu x2 + 9 = 0 ⇒ x2 = -9 ( loại )
Vậy x = -2 thì ( x + 2 )( -x - 5 )( x2 + 9 ) = 0

a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.





 giúp em bài 5 vs ạ
giúp em bài 5 vs ạ